题目内容
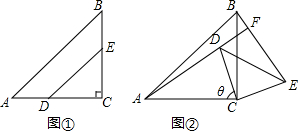
7. 如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.
如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.
分析 根据AE⊥BC于E,AF⊥CD于F,∠EAF=60°,可以得到∠C的度数,由四边形ABCD是平行四边形可以得到∠B、∠D的度数,然后根据解直角三角形的相关知识可以求得AB、BC的长,根据特殊角的三角函数可以求得AE的长,由平行四边形的面积等于底乘以高,可以求得四边形ABCD的面积.
解答 解:∵AE⊥BC,AF⊥CD,∠EAF=60°,
∴∠AEC=∠AFC=90°,
∴∠C=360°-∠AEC-∠EAF-∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,
∴∠B=60°,
∴∠BAE=30°,
∴AB=2BE,
设BE=a,则AB=2a,
∵CE=3cm,FC=1cm,
∴DF=2a-1,
又∵∠AFD=90°,∠D=60°,
∴∠DAF=30°,
∴AD=2DF=4a-2,
∵AD=BC=a+3,
解得a=$\frac{5}{3}$,
∴AB=2a=$\frac{10}{3}$,BC=a+3=$\frac{5}{3}+3=\frac{14}{3}$,
∵∠AEB=90°,AB=$\frac{10}{3}$,BE=$\frac{5}{3}$,
∴AE=$\frac{5\sqrt{3}}{3}$,
∴平行四边形ABCD的面积是:BC•AE=$\frac{14}{3}×\frac{5\sqrt{3}}{3}=\frac{70\sqrt{3}}{9}$,
即AB的长是$\frac{10}{3}$cm,BC的长是$\frac{14}{3}$cm,平行四边形ABCD的面积是$\frac{70\sqrt{3}}{9}c{m}^{2}$.
点评 本题考查平行四边形的性质、平行四边形的面积,30°角所对的直角边和斜边的关系,解题的关键是明确题意,找出所求问题需要的条件.利用数形结合的思想解答问题.

| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
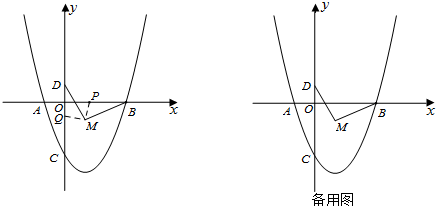
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
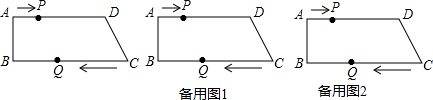
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.
| A. | a>1 | B. | a<1 | C. | a>0 | D. | a≤1 |
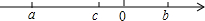 已知,三个实数a,b,c在数轴上的点如图所示,|a-b|+|c-a|-|c+b|的值可能是( )
已知,三个实数a,b,c在数轴上的点如图所示,|a-b|+|c-a|-|c+b|的值可能是( )| A. | 2a | B. | 2b | C. | 2c | D. | -2a |
 如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).
如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).