题目内容
9.已知x1,x2是关于x的一元二次方程x2-4mx+4m2-9=0的两实数根.(1)若这个方程有一个根为-1,求m的值;
(2)若这个方程的一个根大于-1,另一个根小于-1,求m的取值范围;
(3)已知直角△ABC的一边长为7,x1,x2恰好是此三角形的另外两边的边长,求m的值.
分析 (1)把x=-1代入方程,列出m的一元二次方程,求出m的值;
(2)首先用m表示出方程的两根,然后列出m的不等式组,求出m的取值范围;
(3)首先用m表示出方程的两根,分直角△ABC的斜边长为7或2m+3,根据勾股定理求出m的值.
解答 解:(1)∵x1,x2是关于x的一元二次方程x2-4mx+4m2-9=0的两实数根,这个方程有一个根为-1,
∴4m+1=-(4m2-9)
∴m=1或m=-2;
(2)∵x2-4mx+4m2=9,
∴(x-2m)2=9,即x-2m=±3,
∴x1=2m+3,x2=2m-3,
∵2m+3>2m-3,
∴$\left\{\begin{array}{l}{2m+3>-1}\\{2m-3<-1}\end{array}\right.$,解得-2<m<1;
(3)由(2)知道方程x2-4mx+4m2-9=0的两根分别为2m+3,2m-3,
若直角△ABC的斜边长为7,则有49=(2m+3)2+(2m-3)2,解得m=±$\frac{\sqrt{62}}{4}$,
∵边长必须是正数,
∴m=$\frac{\sqrt{62}}{4}$,
若斜边为2m+3,则(2m+3)2=(2m-3)2+72,解得m=$\frac{49}{24}$,
综上m=$\frac{\sqrt{62}}{4}$或m=$\frac{49}{24}$.
点评 本题主要考查了根的判别式与根与系数的关系的知识,解答本题的关键是熟练掌握根与系数关系以及根的判别式的知识,此题难度一般.

练习册系列答案
相关题目
19.-|-3|的值为( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
14.已知m=(-$\frac{\sqrt{3}}{3}$)×(-2$\sqrt{21}$),则有( )
| A. | 5.0<m<5.1 | B. | 5.1<m<5.2 | C. | 5.2<m<5.3 | D. | 5.3<m<5.4 |
1.-3×(-3)=( )
| A. | $\frac{1}{9}$ | B. | -9 | C. | 9 | D. | -$\frac{1}{9}$ |
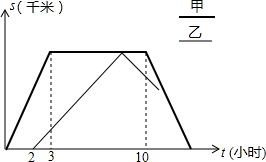 甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:
甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题: