题目内容
14．已知m=（-$\frac{\sqrt{3}}{3}$）×（-2$\sqrt{21}$），则有（ ）| A． | 5.0＜m＜5.1 | B． | 5.1＜m＜5.2 | C． | 5.2＜m＜5.3 | D． | 5.3＜m＜5.4 |
分析 直接利用二次根式的乘法运算法则化简，进而得出m的取值范围．
解答 解：∵m=（-$\frac{\sqrt{3}}{3}$）×（-2$\sqrt{21}$）=2$\sqrt{7}$=$\sqrt{28}$，
5.22=27.04，5.32=28.09，
∴5.2＜m＜5.3．
故选：C．
点评 此题主要考查了二次根式的乘法运算，正确化简是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
5．若反比例函数图象经过二次函数y=x2-4x+7的顶点，则这个反比例函数的解析式为（ ）
| A． | $y=\frac{6}{x}$ | B． | $y=-\frac{6}{x}$ | C． | $y=\frac{14}{x}$ | D． | $y=-\frac{2}{x}$ |
2．一次函数y=x+4与y=-x+b的图象交点不可能在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图，等腰三角形ABC的周长为18，CD为腰AB边上的中线，△ACD与△BCD的周长差为3（AC＞BC），则底边BC的长度是（ ）
6．设某代数式为A，若存在实数x0使得代数式A的值为负数，则代数式A可以是（ ）
| A． | |3-x| | B． | x2+x | C． | $\sqrt{4-x}$ | D． | x2-2x+1 |
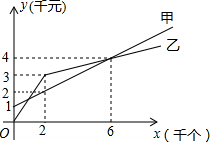某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示．