题目内容
20.学校利用一边靠校园20m的院墙和另外三边用54m长的篱笆围成一块面积为300m2的矩形场地,组织生物小组的学生喂养小动物,在与墙平行的一边开一道1m宽的门,求这块矩形场地的长与宽.分析 设矩形场地的垂直于墙的一边长为xm,而与墙平行的一边开一道1m宽的门,现有能围成54m长的篱笆,那么平行于墙的一边长为(54-2x+1),而矩形场地的面积为300m2,由此即可列出方程,解方程就可以解决问题.
解答 解:设这块矩形场地的垂直于墙的一边长为xm,依题意有
x(54-2x+1)=300,
2x2-55x+300=0,
(x-20)(2x-15)=0,
∴x1=20或x2=7.5,
当x1=20时,54-2x+1=15<20;
当x2=7.5时,54-2x+1=40>20,不合题意舍去.
答:这块矩形场地的长为20m,宽为15m.
点评 此题和实际生活结合比较紧密,正确理解题意,找出题目的数量关系,准确列出方程是解题的关键.此外还要注意判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
5.若反比例函数图象经过二次函数y=x2-4x+7的顶点,则这个反比例函数的解析式为( )
| A. | $y=\frac{6}{x}$ | B. | $y=-\frac{6}{x}$ | C. | $y=\frac{14}{x}$ | D. | $y=-\frac{2}{x}$ |

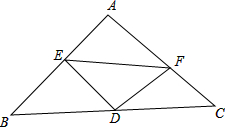 如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.
如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.