题目内容
4.二次函数y=a(x-m)2+k的图象经过(0,5),(12,3)两点,若a<0,0<m<12,则m的值可能是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 根据二次函数图象上点的坐标特征得到$\left\{\begin{array}{l}{a{m}^{2}+k=5①}\\{a(12-m)^{2}+k=3②}\end{array}\right.$,再用加减消元消去k,则可得到m=6+$\frac{1}{12a}$,接着利用a<0得到0<m<6,然后对各选项进行判断.
解答 解:根据题意得$\left\{\begin{array}{l}{a{m}^{2}+k=5①}\\{a(12-m)^{2}+k=3②}\end{array}\right.$,
②-①得a(144-24m)=-2,
所以m=6+$\frac{1}{12a}$,
因为a<0,
所以m<6,即0<m<6.
故选A.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了代数式的变形能力.

练习册系列答案
相关题目
19.$\sqrt{81}$的值等于( )
| A. | 3 | B. | ±3 | C. | ±9 | D. | 9 |
 如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是4cm.
如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是4cm.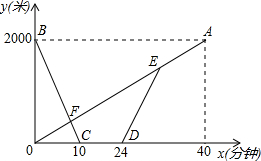 甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图.
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图.