题目内容
6.计算下列各题(1)$(\sqrt{8}+\sqrt{3})×\sqrt{6}$
(2)$\sqrt{12}+\sqrt{27}-\sqrt{\frac{1}{3}}$
(3)$(5\sqrt{3}+2\sqrt{5}{)^2}$
(4)$(3\sqrt{8}+\frac{1}{5}\sqrt{50}-4\sqrt{\frac{1}{2}})÷\sqrt{32}$.
分析 (1)先进行二次根式的乘法运算,然后化简合并;
(2)先进行二次根式的化简,然后合并;
(3)根据完全平方公式求解;
(4)先进行二次根式的除法运算,然后化简合并.
解答 解:(1)原式=$\sqrt{48}$+$\sqrt{18}$
=4$\sqrt{3}$+3$\sqrt{2}$;
(2)原式=2$\sqrt{3}$+3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$;
(3)原式=75+20$\sqrt{15}$+20
=95+20$\sqrt{15}$;
(4)原式=3$\sqrt{\frac{1}{4}}$+$\sqrt{\frac{1}{16}}$-$\sqrt{\frac{1}{4}}$
=1+$\frac{1}{4}$
=$\frac{5}{4}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及乘法运算和除法运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.要使分式$\frac{2}{x-1}$有意义,则x的取值范围为( )
| A. | x>1 | B. | x≥1 | C. | x≠1 | D. | x=1 |
14.下列各式正确的是( )
| A. | $\sqrt{{{(-5)}^2}}=-5$ | B. | $-\sqrt{{{(-15)}^2}}=-15$ | C. | $\sqrt{{{(-5)}^2}}=±5$ | D. | $\sqrt{\frac{1}{2}}=\frac{1}{2}$ |
1.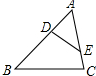 如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
 如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
11.已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3等于( )
| A. | 150° | B. | 180° | C. | 210° | D. | 120° |
16.下列多项式不是完全平方式的是( )
| A. | x2+4x+4 | B. | $\frac{1}{4}$x2-x+1 | C. | 4x2+4x+1 | D. | x2-2x+$\frac{1}{4}$ |
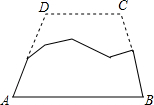 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角分别是多少度?
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角分别是多少度?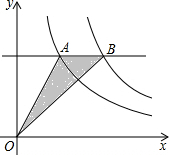 如图,是反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲于A、B两点,若S△AOB=2,则k2-k1的值是( )
如图,是反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲于A、B两点,若S△AOB=2,则k2-k1的值是( )