题目内容
15.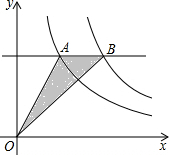 如图,是反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲于A、B两点,若S△AOB=2,则k2-k1的值是( )
如图,是反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲于A、B两点,若S△AOB=2,则k2-k1的值是( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
分析 设A(a,b),B(c,d),代入双曲线得到k1=ab,k2=cd,根据三角形的面积公式求出cd-ab=4,即可得出答案.
解答 解:设A(a,b),B(c,d),
代入得:k1=ab,k2=cd,
∵S△AOB=2,
∴$\frac{1}{2}$cd-$\frac{1}{2}$ab=2,
∴cd-ab=4,
∴k2-k1=4,
故答案为:4.
点评 本题主要考查了对反比例函数系数的几何意义,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,能求出cd-ab=4是解此题的关键.

练习册系列答案
相关题目
10.解方程:$\frac{x}{3}=1-\frac{x-1}{4}$去分母后正确的是( )
| A. | 4x=1-3(x-1) | B. | x=1-(x-1) | C. | 4x=3-(x-1) | D. | 4x=12-3(x-1) |
20. 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )
 如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内点A、点B分别对应点C、点D,且S△OCD:S△OAB=1:4,则端点D的坐标为( )| A. | (2,1) | B. | (2,2) | C. | (3,1) | D. | (3,2) |
4.某种细胞开始分裂时有两个,1小时后分裂成4个并死去一个,2小时后分裂成6个并死去一个,3小时后分裂成10并死去一个,按此规律,10小时后细胞存活的个数是( )
| A. | 1023 | B. | 1024 | C. | 1025 | D. | 1026 |
5.在平面直角坐标系中,已知点P的坐标为(5,12),则OP的长为( )
| A. | 5 | B. | 12 | C. | 13 | D. | 14 |