题目内容
7. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.
如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.
分析 首先根据平行线的性质求出∠3的度数,然后根据三角形的外角的知识求出∠A的度数.
解答  解:如图,∵直线m∥n,
解:如图,∵直线m∥n,
∴∠1=∠3,
∵∠1=70°,
∴∠3=70°,
∵∠3=∠2+∠A,∠2=30°,
∴∠A=40°,
故答案为:40°.
点评 本题考查了平行线的性质和三角形的外角性质,关键是运用三角形外角的性质,求出∠3的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.某商场经营一批进价是30元/件的商品,在市场试销中的日销售量y件与销售价x元之间满足一次函数关系.?
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;?
(2)若日销售利润为P元,根据上述关系写出P关于x的函数关系式,并指出当销售单价x为多少元时,才能获得最大的销售利润?
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;?
| x | 35 | 40 | 45 | 50 |
| y | 57 | 42 | 27 | 12 |
18.某超市在50天内试销一款成本40元/件的新型商品,了解到此款商品第x天的销售信息如下表:
(1)当第5或45天时,该商品的销售单价为65元/件;
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
| 销售量P(件) | p=120-2x |
| 销售单价q(元/件) | 当1≤x<25时,q=x+60; 当25≤x≤50时,q=40+$\frac{1125}{x}$ |
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
16.农民购买农机设备政府会给予一定额度的补贴,其中购买Ⅰ、Ⅱ型农机设备的金额与政府补贴的金额存在表所示的函数对应关系:
(1)分别求出y1和y2的函数解析式;
(2)张大伯打算共用10万元购买Ⅰ、Ⅱ两型农机设备.请你帮助张大伯设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
| 型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
| 购买金额x(万元) | x | 1 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx(k≠0) | 0.4 | y2=ax2+bx(a≠0) | 2.4 | 3.2 |
(2)张大伯打算共用10万元购买Ⅰ、Ⅱ两型农机设备.请你帮助张大伯设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
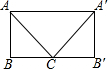
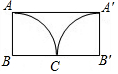
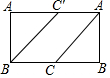
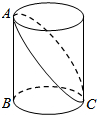 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )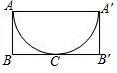
 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.