题目内容
5.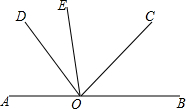 如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.
如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.(1)若∠AOE=90°,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠AOD的度数.
分析 (1)根据∠AOE=90°和∠AOE=∠COD求出∠COD的度数,求出∠AOD,即可求出答案;
(2)根据角平分线定义得出∠COE=∠BOC,求出∠AOD=∠EOC=∠BOC,根据∠AOD+∠DOE+∠EOC+∠BOC=180°求出即可.
解答 解:(1)∵∠AOE=90°,∠AOE=∠COD,
∴∠COD=∠AOE=90°,
∵∠EOD=30°,
∴∠AOD=90°-30°=60°,
∴∠BOC=180°-∠DOC-∠AOD=180°-90°-60°=30°;
(2)∵OC平分∠BOE,
∴∠COE=∠BOC,
∵∠AOE=∠COD,
∴∠AOD+∠DOE=∠DOE+∠EOC,
∴∠AOD=∠EOC=∠BOC,
∵∠AOD+∠DOE+∠EOC+∠BOC=180°,∠EOD=30°,
∴∠AOD=50°.
点评 本题考查了角的有关计算和角平分线定义,能求出各个角的度数是解此题的关键.

练习册系列答案
相关题目
13.一元二次方程:x2-9=0的解是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |

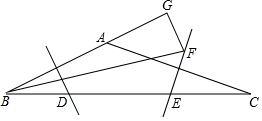 如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.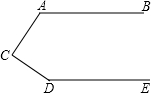 如图,AB∥DE,∠A=120°,∠C=80°,则∠D的度数为160°.
如图,AB∥DE,∠A=120°,∠C=80°,则∠D的度数为160°. .
.