题目内容
2. 已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )①∠PAD=∠PDA=60°;
②△PAO≌△ADE;
③PO=$\sqrt{2}$r;
④AO:OP:PA=1:$\sqrt{2}$:$\sqrt{3}$.
| A. | ①④ | B. | ②③ | C. | ③④ | D. | ①③④ |
分析 由⊙O的六等分点得出$\widehat{AE}=\widehat{DF}$,得出AE=DF<AD,根据题意得:AP=AE,DP=DF,得出AP=DP<AD,△PAD是等腰三角形,∠PAD=∠PDA≠60°,①错误;连接OP、AE、DE,由AD>AE=AP得出②△PAO≌△ADE错误,由圆周角定理得出∠AED=90°,∠DAE=30°,得出DE=r,AE=$\sqrt{3}$DE=$\sqrt{3}$r,得出AP=AE=$\sqrt{3}$r,
由等腰三角形的性质得出PO⊥AD,由勾股定理求出PO=$\sqrt{A{P}^{2}-O{A}^{2}}$=$\sqrt{2}$r,③正确;求出AO:OP:PA=1:$\sqrt{2}$:$\sqrt{3}$.得出④正确;即可得出结论.
解答 解:∵A、B、C、D、E、F是半径为r的⊙O的六等分点,
∴$\widehat{AE}=\widehat{DF}$,
∴AE=DF<AD,
根据题意得:AP=AE,DP=DF,
∴AP=DP<AD,
∴△PAD是等腰三角形,∠PAD=∠PDA≠60°,①错误;
连接OP、AE、DE,如图所示,
∵AD是⊙O的直径,
∴AD>AE=AP,②△PAO≌△ADE错误,∠AED=90°,∠DAE=30°,
∴DE=r,AE=$\sqrt{3}$DE=$\sqrt{3}$r,
∴AP=AE=$\sqrt{3}$r,
∵OA=OD,AP=DP,
∴PO⊥AD,
∴PO=$\sqrt{A{P}^{2}-O{A}^{2}}$=$\sqrt{2}$r,③正确;
∵AO:OP:PA=r:$\sqrt{2}$r:$\sqrt{3}$r=1:$\sqrt{2}$:$\sqrt{3}$.
∴④正确;
说法正确的是③④,
故选:C.
点评 本题是圆的综合题目,考查了圆心角、弧、弦的关系,圆周角定理,等腰三角形的判定、勾股定理等知识;本题综合性强,有一定难度,熟练掌握圆周角定理是解决问题的关键.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | $\left\{\begin{array}{l}{x+y=52}\\{3x+2y=20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=52}\\{2x+3y=20}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=20}\\{2x+3y=52}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=20}\\{3x+2y=52}\end{array}\right.$ |
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $3\sqrt{6}$ | D. | $9\sqrt{2}$ |
| A. | 4、5、10 | B. | 12、12、1 | C. | 3、8、5 | D. | 3、3、7 |
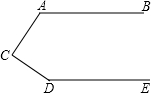 如图,AB∥DE,∠A=120°,∠C=80°,则∠D的度数为160°.
如图,AB∥DE,∠A=120°,∠C=80°,则∠D的度数为160°. .
. 如图,在直角坐标系中,△ABC的顶点坐标分别为A(-6,0),B(2,0),C(-1,8),求△ABC的面积.
如图,在直角坐标系中,△ABC的顶点坐标分别为A(-6,0),B(2,0),C(-1,8),求△ABC的面积.