题目内容
8. 如图,AC是⊙O的弦,OF⊥AC于点F,延长OF,与过点A的切线交于点P,若∠P=30°,AP=$\sqrt{3}$,则OF的值是( )
如图,AC是⊙O的弦,OF⊥AC于点F,延长OF,与过点A的切线交于点P,若∠P=30°,AP=$\sqrt{3}$,则OF的值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 首先由切线的性质,利用锐角三角函数可得OA,在直角三角形中OAF中,利用直角三角形的性质可得OF.
解答 解:∵OF⊥AC于点F,AP为⊙O的切线,∠P=30°,
∴OA=AP•tan30°=$\sqrt{3}×\frac{\sqrt{3}}{3}$=1,
∵∠P=30°,∠OAP=90°,
∴∠O=60°,
∴∠OAF=30°,
∴OF=$\frac{1}{2}OA$=$\frac{1}{2}×1=\frac{1}{2}$,
故选A.
点评 本题主要考查了三角函数和切线的性质,利用三角函数求得OA是解答此题的关键.

练习册系列答案
相关题目
16.-8的立方根是( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |
17.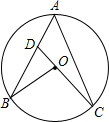 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,四边形DECB的面积是10,则△ABC的面积为( )
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,四边形DECB的面积是10,则△ABC的面积为( )
 如图是由5个大小相同的小正方体组成的几何体,则其俯视图是( )
如图是由5个大小相同的小正方体组成的几何体,则其俯视图是( )



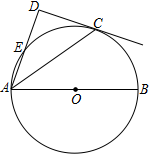 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.