题目内容
2.若y=(m+1)x|m+2|-2n+8是正比例函数,(1)求m、n的值;
(2)写出y与x的函数关系.
分析 (1)根据正比例函数的定义,指数为1,系数不为0,常数项为0,计算即可得出m,n的值;
(2)把m、n的值代入即可得出答案.
解答 解:(1)∵y=(m+1)x|m+2|-2n+8是正比例函数,
∴|m+2|=1且m+1≠0,-2n+8=0,
解得m=-1或-3且m≠-1,n=4,
∴m的值为-3,n的值为4;
(2)把m=-3,n=4代入y=(m+1)x|m+2|-2n+8得y与x的函数关系式为y=-2x.
点评 本题考查了正比例函数的定义,一般地,两个变量x,y之间的关系式可以表示成形如y=kx(k为常数,且k≠0)的函数,那么y就叫做x的正比例函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若x2-5x+6=(x+a)(x+b),a,b的值可能为( )
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
 一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.
一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.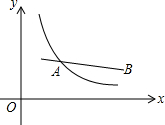 如图,已知线段AB,点A的坐标为(1,$\frac{3}{2}$),点B的坐标为(4,1),反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB有交点,则k的取值范围为$\frac{3}{2}$≤k≤4.
如图,已知线段AB,点A的坐标为(1,$\frac{3}{2}$),点B的坐标为(4,1),反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB有交点,则k的取值范围为$\frac{3}{2}$≤k≤4.