题目内容
12.某阀门工厂生产A,B两种阀门零件.(1)在规定的时间内该工厂需生产A、B两种阀门零件共9000个,其中,B零件个数是A零件个数的2倍多900个.
①根据上述信息求A,B零件的生产个数;
②如果工厂安排24人同时生产这两种零件,每人每天能生产A零件90个或B零件150个,应分别安排多少人生产A零件和B零件,才能确保在几天后同时完成A,B两种阀门零件的生产任务?
(2)已知生产A,B零件的投入分别为10元/个,15元/个,生产A,B两种零件的次品率均为10%,为了使得A,B零件的正品数能达到问题(1)中的个数要求,工厂恰投入135060元进行生产,则工厂总共可能生产了10004或10005或10006个零件.(直接写出答案)(次品率=$\frac{次品数}{生产总数}×100%$)
分析 (1)①设A零件个数为x个,B零件有y个,根据:A零件数+B零件数=9000、B零件数=A零件数×2+900,列方程组求解可得;
②设安排m人生产A零件,则生产B零件的有(24-m)人,根据:生产A零件所需时间=生产B零件所需时间,列方程求解可得;
(2)根据:生产A零件总费用+生产B零件总费用=135060及A零件正品数≥2700、B零件正品数≥6300,确定x、y间的关系,列出所有可能取值即可知总数.
解答 解:(1)①设A零件个数为x个,则B零件有y个,
根据题意,得:$\left\{\begin{array}{l}{x+y=9000}\\{y=2x+900}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2700}\\{y=6300}\end{array}\right.$
答:A零件的生产个数为2700个,B零件的生产个数位6300个;
②设安排m人生产A零件,则生产B零件的有(24-m)人,
根据题意,得:$\frac{6300}{150(24-m)}$=$\frac{2700}{90m}$,
解得:m=10,
经检验m=10是原方程的根,
则24-m=14(人);
(2)设生产A零件x个,生产B零件y个,
则10x+15y=135060,且0.9x≥2700,0.9y≥6300,
即:2x+3y=27012,且x≥3000,y≥7000,
∴当x=3000时,y=7004,共生产10004个,
当x=3003时,y=7002,共生产10005个,
当x=3006时,y=7000,共生产10006个,
故答案为:10004或10005或10006.
点评 本题主要考查二元一次方程、分式方程的应用能力,结合题意确定相等关系,并根据相等关系列出方程或方程组是解题关键.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案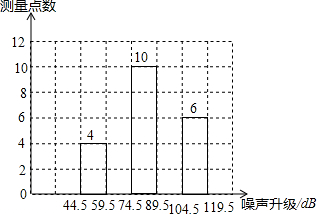 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
(1)表中的c值为0.3;
(2)补全频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳高运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系)
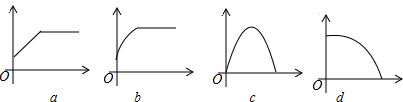
| A. | abcd | B. | dabc | C. | dbca | D. | cabd |
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.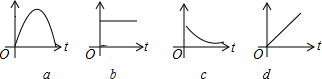
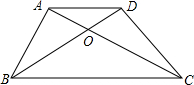 如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.