题目内容
14.已知方程组$\left\{\begin{array}{l}{x+y=3}\\{ax-2y=4b}\end{array}\right.$与方程组$\left\{\begin{array}{l}{x+2y=4}\\{3bx+ay=3a-b}\end{array}\right.$有相同解,求a+b的值.分析 根据有相同的解,取每个方程组的第一个方程组成方程组,求出x和y的值;将x和y的值代入另外两个方程,组成方程组,解方程组即可求出a+b的值.
解答 解:根据题意,得:$\left\{\begin{array}{l}{x+y=3}\\{x+2y=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入ax-2y=4b和3bx+ay=3a-b,得$\left\{\begin{array}{l}{2a-2=4b}\\{6b+a=3a-b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{7}{3}}\\{b=\frac{2}{3}}\end{array}\right.$.
则a+b=$\frac{7}{3}+\frac{2}{3}=3$.
点评 本题主要考查二元一次方程组的解,能熟练解方程组是解决此题的基础,取每个方程组的第一个方程组成方程组,求出x和y的值是解决此题的关键.

练习册系列答案
相关题目

 如图,已知DB∥FG∥EC,∠ABD=60°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.
如图,已知DB∥FG∥EC,∠ABD=60°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.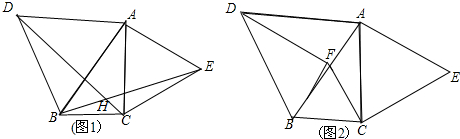
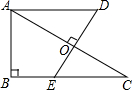 如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为$\frac{169}{24}$.
如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为$\frac{169}{24}$.