题目内容
13.已知关于x的一元二次方程(a-c)x2-2bx+(a+c)=0,其中a、b、c分别为△ABC三边的长.(1)如果x=1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
分析 (1)根据根的定义,把x=1代入即可得出△ABC的形状;
(2)根据根的判别式得出b2-4ac=0,即可得出a,b,c的关系,即可根据勾股定理的逆定理判断△ABC的形状.
解答 解:(1)∵x=1是一元二次方程(a-c)x2-2bx+(a+c)=0的根,
∴(a-c)-2b+(a+c)=0,
∴a=b,
∵a-c≠0,
∴a≠c,
∴△ABC为等腰三角形;
(2)∵方程有两个相等的实数根,
∴b2-4ac=0,
即4b2-4(a+c)(a-c)=0,
∴b2+c2=a2,
∴△ABC为直角三角形.
点评 本题考查了根的判别式以及一元二次方程、等腰三角形的判定、直角三角形的判定,掌握各个定理的内容是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.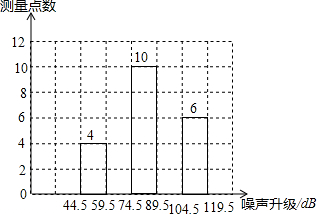 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
根据表中提供的信息解答下列问题:
(1)表中的c值为0.3;
(2)补全频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
 为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
为了增强人们的环境保护意识,某校若干名学生组成了“控制噪声污染”课题学习研究小组.在环保局工作人员帮助指导下,该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
(1)表中的c值为0.3;
(2)补全频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
18.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是( )
| A. | 12cm2 | B. | 96cm2 | C. | 48cm2 | D. | 24cm2 |
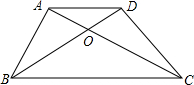 如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.