题目内容
13.长、宽、高分别为4cm、3cm、12cm的长方体纸盒内可完全放入的棍子最长是13cm.分析 根据题意画出图形,两次运用勾股定理即可得出结果.
解答 解:如图所示: BC=3cm,CD=4cm,AB=12cm,
BC=3cm,CD=4cm,AB=12cm,
连接BD、AD,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5(cm),
在Rt△ABD中,AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13(cm).
故这个盒子最长能放13cm的棍子.
故答案为:13.
点评 本题考查的是勾股定理的应用,根据题意画出图形,作出辅助线、构造出直角三角形是解答此题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
1.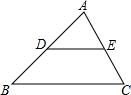 如图所示,在△ABC中,点D、E分别是边AB、AC的中点,则△ADE和△ABC的周长之比等于( )
如图所示,在△ABC中,点D、E分别是边AB、AC的中点,则△ADE和△ABC的周长之比等于( )
 如图所示,在△ABC中,点D、E分别是边AB、AC的中点,则△ADE和△ABC的周长之比等于( )
如图所示,在△ABC中,点D、E分别是边AB、AC的中点,则△ADE和△ABC的周长之比等于( )| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |