题目内容
4.若3x2m-1与-2x3y2n-3是同类项,且|a-2m|+(0.5b-n)2=0,则m+n+a+b的值为$\frac{11}{2}$.分析 根据同类项的概念求出m、n的值,然后根据非负数的性质求出a、b的值,最后代入求解.
解答 解:∵3x2m-1与-2x3y2n-3是同类项,
∴2m-1=3,2n-3=0,
解得:m=2,n=$\frac{3}{2}$,
∵|a-2m|+(0.5b-n)2=0,
∴a=2m,0.5b=n,
即a=4,b=3,
则m+n+a+b=2+$\frac{3}{2}$+4+3=$\frac{11}{2}$.
故答案为:$\frac{11}{2}$.
点评 本题考查了同类项和非负数的性质,解答本题的关键是掌握同类项的概念以及非负数的性质.

练习册系列答案
相关题目
19.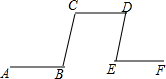 如图,AB∥CD∥EF,BC∥DE,则∠B与∠E的关系是( )
如图,AB∥CD∥EF,BC∥DE,则∠B与∠E的关系是( )
 如图,AB∥CD∥EF,BC∥DE,则∠B与∠E的关系是( )
如图,AB∥CD∥EF,BC∥DE,则∠B与∠E的关系是( )| A. | 相等 | B. | 互余 | C. | 互补 | D. | 不能确定 |
