题目内容
1.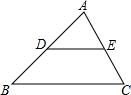 如图所示,在△ABC中,点D、E分别是边AB、AC的中点,则△ADE和△ABC的周长之比等于( )
如图所示,在△ABC中,点D、E分别是边AB、AC的中点,则△ADE和△ABC的周长之比等于( )| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
分析 D、E分别是AB、AC边的中点,则DE是△ABC的中位线;根据三角形的中位线平行于第三边,且等于第三边的一半,因而中位线分三角形得到的小三角形与原三角形一定相似,且相似是1:2,然后根据相似三角形的周长比等于相似比即可求解.
解答 解:∵点D,点E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE:BC=1:2,
∴△ADE∽△ABC,
∴△ADE与△ABC的周长比为1:2.
故选C.
点评 本题主要考查了三角形的中位线定理以及相似三角形的判定与性质,熟练掌握三角形的中位线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.等腰三角形的周长为13,各边长均为整数,则这样的三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |

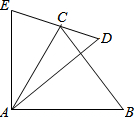 如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.
如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B. 我班几名同学用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案如图所示:那么第2014个图案中有白色纸片6043张.
我班几名同学用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案如图所示:那么第2014个图案中有白色纸片6043张.