Question

11．如图，等腰Rt△ABC中，∠A=90°，L为BC中点，LOVE为正方形且V在AC上，若BO=$\sqrt{3}$CE，BC=4，求正方形LOVE的面积．

Answer 1

分析 注意到∠VCL=$\frac{1}{2}$∠VEL，EV=EL，由此得出EC=EV=EL，过点O、E作BC垂线，垂足分别为H、G，则易证△OHL≌△LGE，从而算出OH=LG=GC=1，
设正方形的边长为x，利用BH+HL=2建立方程，求出x的平方即可．

解答 解：∵∠VCL=$\frac{1}{2}$∠VEL，EV=EL，
∴点C在以E为圆心EV为半径的圆周上，
即EC=EV=EL，
过点O、E作BC垂线，垂足分别为H、G，如图，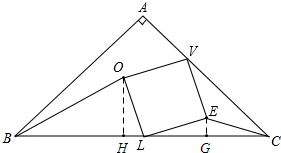

则LG=GC，
∵∠HOL+∠OLH=90°=∠OLH+∠GLE，
∴∠HOL=∠GLE，
在△OHL和△LGE中，
$\left\{\begin{array}{l}{∠OHL=∠LGE}\\{∠HOL=∠GLE}\\{OL=LE}\end{array}\right.$
∴△OHL≌△LGE，
设正方形OLEV的边长为x，则BO=$\sqrt{3}$x，
而OH=LG=CG=$\frac{1}{2}$CL=1，
∴$\sqrt{3{x}^{2}-1}+\sqrt{{x}^{2}-1}=2$，
解得x²=4±2$\sqrt{2}$，
∴正方形LOVE的面积为4-2$\sqrt{2}$．

点评 本题主要考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定与性质、勾股定理、解无理方程等重要知识点，难度较大，是一个经典几何好题．观察到∠VCL=$\frac{1}{2}$∠VEL，EV=EL，从而得出EC=EV=EL是解决本题的突破口和关键．