Question

3．如图，在△ABC中，∠C=90°，O是BC上一点，以O为圆心，OC为半径的圆过AB上一点D．
（1）若AD=AC，求证：AB是⊙O的切线；
（2）若BE=4，BD=8，求CE和AD的长．

Answer 1

分析 （1）连接OD，如图，证明△AOC≌△AOD得到∠ACO=∠ADO=90°，然后根据切线的判定方法可判断AB是⊙O的切线；
（2）设⊙O的半径为r，则OB=r+4，在Rt△OBD中利用勾股定理得到∴r²+8²=（r+4）²，解方程求出r即可得到CE的长，设AD=AC=t，然后在Rt△ACB中利用勾股得到t²+16²=（t+8）²，再解方程即可．

解答 （1）证明：连接OD，如图，
在△AOC和△AOD中
$\left\{\begin{array}{l}{AO=AO}\\{AC=AD}\\{OC=OD}\end{array}\right.$，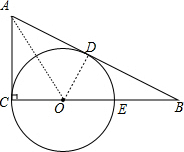
∴△AOC≌△AOD，
∴∠ACO=∠ADO=90°，
∴OD⊥AB，
∴AB是⊙O的切线；
（2）解：设⊙O的半径为r，则OB=r+4，
在Rt△OBD中，∵OD²+BD²=OB²，
∴r²+8²=（r+4）²，解得r=6，
∴CE=2r=12，
∵△AOC≌△AOD，
∴AC=AD，
设AD=t，
在Rt△ACB中，∵AC²+BC²=AB²，
∴t²+16²=（t+8）²，解得t=20，
即AD=20．

点评 本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．