题目内容
3. 已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=$\sqrt{21}$,AD=2,试判断A、B、C、D四点是否在同一个圆上,并说明理由.
已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=$\sqrt{21}$,AD=2,试判断A、B、C、D四点是否在同一个圆上,并说明理由.
分析 根据勾股定理和勾股定理的逆定理即可得到结论.
解答  解:
解:
在,
理由:连接AC,
∵∠B=90°,
∴AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=5,
∵AD2+CD2=25=AC2,
∴∠D=90°,
∴∠B+∠D=180°,
∴A、B、C、D四点在同一个圆上.
点评 本题考查了圆周角定理,90度的圆周角所对的弦是直径,理解定理是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.已知△ABC的三个顶点A(5,6)、B(7,2)、C(4,3),先将△ABC向左平移一个单位,再以原点O为位似中心,在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段△A′B′C′,则点A的对应点A′的坐标为( )
| A. | (2,1) | B. | (3,1) | C. | (2,3) | D. | (3,3) |
11. 下列图中,与图中由实线围成的图形成全等形的是( )
下列图中,与图中由实线围成的图形成全等形的是( )
 下列图中,与图中由实线围成的图形成全等形的是( )
下列图中,与图中由实线围成的图形成全等形的是( )| A. |  | B. |  | C. |  | D. |  |
18.第31届夏季奥林匹克运动会,又称2016年里约热内卢奥运会,于2016年8月5日至8月21日在巴西的里约热内卢举行,奥运会期间,某吉祥物店在一周的销售中,盈亏情况如表(盈余为正,单位:万元)
表中星期五的盈亏数被墨水涂污了,请你算出星期五的盈亏数,并说明星期五是盈还是亏?盈亏是多少万元?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
| -25.6 | -72.7 | 200 | -4 | 128.3 | 168 | 494 |
8.一个数x的相反数的绝对值为3,则这个数是( )
| A. | 3 | B. | -3 | C. | |-x| | D. | ±3 |
15.三条直线l1,l2,l3相互交叉,交点分别为A,B,C,在平面内找一个点,使它到三条直线的距离相等,则这样的点共有( )
| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
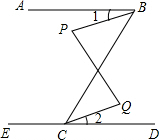 如图,已知∠ABC+∠ECB=180°,∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
如图,已知∠ABC+∠ECB=180°,∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
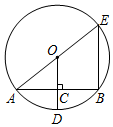 如图,如AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,则BE=6cm.
如图,如AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,则BE=6cm.