题目内容
15．三条直线l1，l2，l3相互交叉，交点分别为A，B，C，在平面内找一个点，使它到三条直线的距离相等，则这样的点共有（ ）| A． | 一个 | B． | 两个 | C． | 三个 | D． | 四个 |
分析 作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线，外角平分线相交于点P1、P2、P3，内角平分线相交于点P4，然后根据角平分线的性质进行判断．
解答 解：作直线l1、l2、l3所围成的△ABC的外角平分线和内角平分线，
内角平分线相交于点P1，外角平分线相交于点P2、P3、P4，
根据角平分线的性质可得，这4个点到三条直线的距离分别相等．
故选：D．
点评 本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
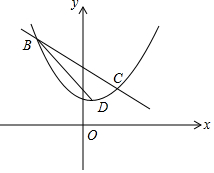在平面直角坐标系xOy中，抛物线y=ax2+bx+2的顶点为D（1，$\frac{3}{2}$），
已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=$\sqrt{21}$，AD=2，试判断A、B、C、D四点是否在同一个圆上，并说明理由．
已知AB=DC，BE=CF，只要补充∠B=∠C，或AB∥CD，就可以证明△ABE≌△DCF．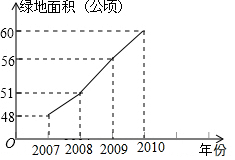
美化城市，改善人们的居住环境已成为城市建设的一项重要内容．某市城区近几年来，通过拆迁旧房、植树、种草、修建公园等措施，使城区绿地面积不断增加（如图所示）．