题目内容
19.先化简,再求值:$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$÷($\frac{1}{a}$-$\frac{1}{b}$),其中a=$\sqrt{3}$+1,b=$\sqrt{3}$-1.分析 先化简题目中的式子,然后将a、b的值代入化简后的式子即可解答本题.
解答 解:$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$÷($\frac{1}{a}$-$\frac{1}{b}$)
=$\frac{(a-b)^{2}}{(a+b)(a-b)}÷\frac{b-a}{ab}$
=$\frac{(a-b)^{2}}{(a+b)(a-b)}•\frac{ab}{b-a}$
=$-\frac{ab}{a+b}$,
当a=$\sqrt{3}$+1,b=$\sqrt{3}$-1时,原式=$-\frac{(\sqrt{3}+1)(\sqrt{3}-1)}{\sqrt{3}+1+\sqrt{3}-1}$=-$\frac{3-1}{2\sqrt{3}}$=$-\frac{\sqrt{3}}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.列方程组解应用题,根据国家发改委实施“阶梯电价”的有关文件要求,某市决定从2012年6月1日起对居民生活用电试行“阶梯电价”的收费,具体收费标准见下表:若该市一户居民6月份用电320千瓦时,应缴电费164元,7月份用电450千瓦时,应缴电费248元,求a、b的值.
| 一户居民一个月用电量的范围 | 电费价格(单位:元千瓦时) |
| 不超过240千瓦时的部分 | a |
| 超过240千瓦时,但不超过400千瓦时的部分 | b |
| 超过400千瓦时的部分 | a+0.3 |
 如图,已知平行四边形ABCD中,△DEC和△FBC是等边三角形,则∠AEF=60°.
如图,已知平行四边形ABCD中,△DEC和△FBC是等边三角形,则∠AEF=60°.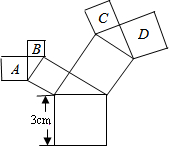 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2.