题目内容
9.“六一儿童节”即将结束,某幼儿园计划采购一批市场价为20元/件的益智玩具,甲、乙两家工厂给出了不同的优惠方案,方案如下:甲工厂:采购金额超过500元后,超过的部分按九折付款;
乙工厂:采购金额超过1000元后,超过的部分按八折付款.
(1)如果幼儿园采购的数量超过了50件,应该到哪家工厂进行采购更合算?
(2)如果幼儿园选择到乙工厂进行采购,那么幼儿园至少应该采购多少件,才能使每件玩具的平均价格不超过18元?
分析 (1)设幼儿园计划采购益智玩具x件,选择甲工厂时费用为y1,选择乙工厂时费用为y2,由采购的优惠条件分别得到y1=18x+50,y2=16x+200.分三种情况讨论:甲=乙,甲>乙,甲<乙;
(2)设幼儿园到乙工厂采购益智玩具x件,由题意得16x+200≤18x,解该不等式即可.
解答 解:(1)∵20×50=1000(元),
∴幼儿园到两家工厂采购均可得到优惠.
设幼儿园计划采购益智玩具x件,选择甲工厂时费用为y1,选择乙工厂时费用为y2,由题意得
y1=500+0.9(20x-500)=18x+50.
y2=1000+0.8(20x-1000)=16x+200.
由y1=y2,得18x+50=16x+200,解得x=75.
由y1<y2,得18x+50<16x+200,解得x<75.
由y1>y2,得18x+50>16x+200,解得x>75.
∵采购的数量超过了50件,
∴当采购的数量为50<x<75时,选择甲工厂时费用较低.
当采购的数量为75件时,选择两家工厂的费用一样.
当采购的数量为x>75时,选择乙工厂时费用较低.
(2)设幼儿园到乙工厂采购益智玩具x件,由题意得
16x+200≤18x,
解得x≥100.
所以,该幼儿园到乙工厂至少采购100件时,才能能使每件玩具的平均价格不超过18元.
点评 本题考查了一元一次不等式的应用.关键是根据列不等式以及数学实际问题中的方案设计及实惠问题解答.

练习册系列答案
相关题目
18.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的有( )
①$\frac{c}{a}$=6;②函数y=ax2+bx+c的最小值为-6;③抛物线的对称轴是x=$\frac{7}{2}$;④方程ax2+bx+c=0有两个正整数解.
| x | … | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 0 | -3 | -6 | -6 | -3 | … |
①$\frac{c}{a}$=6;②函数y=ax2+bx+c的最小值为-6;③抛物线的对称轴是x=$\frac{7}{2}$;④方程ax2+bx+c=0有两个正整数解.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,平行四边形ABCD内有一点E,满足ED⊥AD,且∠EBC=∠EDC,BE=CD.证明:∠ECB=45°.
如图,平行四边形ABCD内有一点E,满足ED⊥AD,且∠EBC=∠EDC,BE=CD.证明:∠ECB=45°. 如图,将长方形ABCD分割成1个灰色长方形与52个边长为1的小正方形,若灰色长方形的长与宽之比为7:5,则灰色长方形的长为14.
如图,将长方形ABCD分割成1个灰色长方形与52个边长为1的小正方形,若灰色长方形的长与宽之比为7:5,则灰色长方形的长为14. 欣赏图所示的团,并用两种方法分析图案的形成过程.
欣赏图所示的团,并用两种方法分析图案的形成过程.
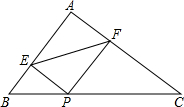 如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为4.8.
如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为4.8.