题目内容
7.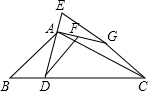 如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则$\frac{AB}{CG}$的值为$\frac{\sqrt{3}+1}{2}$.
如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则$\frac{AB}{CG}$的值为$\frac{\sqrt{3}+1}{2}$.
分析 过点A作AH⊥BC于点H,过点G作GK⊥BC于K,过点A作AL⊥GK于点L,取AC中点M,连接GM.首先证明Rt△ADF≌Rt△AGE,△ADH≌△AGL≌△AGM,推出∠DAH=∠GAM=∠GAL=∠ACG=15°,设AH=a,则CD=AC=2a,CH=$\sqrt{3}$a,分别用a表示AB、CG即可解决问题.
解答 解:过点A作AH⊥BC于点H,过点G作GK⊥BC于K,过点A作AL⊥GK于点L,取AC中点M,连接GM.
∵AG⊥DE,
∴∠DAF=∠EAG=90°
在Rt△ADF和Rt△AGE中,
$\left\{\begin{array}{l}{AF=AE}\\{DF=EG}\end{array}\right.$,
∴Rt△ADF≌Rt△AGE,
∴AD=AG,
∵∠AHK=∠ALK=∠LKH=90°,
∴四边形AHKL是矩形,
∴∠DAG=∠HAL=90°,
∴∠DAH=∠GAL,∵∠AHD=∠ALG=90°,
∴△ADH≌△AGL,
∴AH=AL,
在Rt△ACH中,∵∠ACH=30°,
∴AH=AL=$\frac{1}{2}$AC=AM,
∵AG=AG,∠ALG=∠AMG=90°,
∴Rt△AGM≌Rt△AGL,
∴∠GAL=∠GAM,
∵AL∥BC,
∴∠CAL=∠ACH=30°,
∴∠GAL=∠GAM=15°,
∴∠DAH=∠GAL=15°,
∴∠CAD=∠CDA=75°,
∴AC=AD,设AH=a,则CD=AC=2a,CH=$\sqrt{3}$a,
∴LG=DH=CD-CH=2a-$\sqrt{3}$a,
∴GK=LK-LG=($\sqrt{3}$-1)a,
∵GA=GC,
∴∠GAC=∠GCA=15°,
∴∠GCK=45°,
∴CG=$\sqrt{2}$KG=($\sqrt{6}$-$\sqrt{2}$)a,∵AB=$\sqrt{2}$AH=$\sqrt{2}$a,
∴$\frac{AB}{CG}$=$\frac{\sqrt{2}a}{(\sqrt{6}-\sqrt{2})a}$=$\frac{\sqrt{3}+1}{2}$.
故答案为$\frac{\sqrt{3}+1}{2}$.
点评 本题考查全等三角形的判定和性质、矩形的判定和性质、勾股定理、30度角的直角三角形的性质、等腰直角三角形的性质的等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案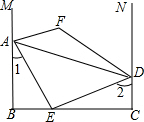 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值
其中结论正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 下列数学家中,用如图所示的“弦图”证明了勾股定理的是( )
下列数学家中,用如图所示的“弦图”证明了勾股定理的是( )| A. | 刘徽 | B. | 赵爽 | C. | 祖冲之 | D. | 秦九韶 |
| A. | 1 | B. | -27 | C. | 1或-27 | D. | 1或27 |
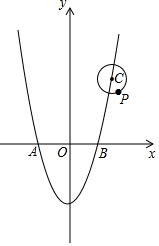 【材料阅读】阅读下列一段文字,然后回答下列问题.
【材料阅读】阅读下列一段文字,然后回答下列问题.