题目内容
2.先化简,再求值$\frac{1}{x+1}-\frac{1}{{{x^2}-1}}÷\frac{x+1}{{{x^2}-2x+1}}$,其中$x=\sqrt{2}-1$.分析 先算除法,再算减法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{1}{x+1}$-$\frac{1}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+1}$
=$\frac{1}{x+1}$-$\frac{x-1}{(x+1)^{2}}$
=$\frac{x+1-x+1}{{(x+1)}^{2}}$
=$\frac{2}{{(x+1)}^{2}}$,
当x=$\sqrt{2}$-1时,原式=$\frac{2}{{(\sqrt{2}-1+1)}^{2}}$=1.
点评 本题考查的是分式的化简求值,在解答此类题目时要注意把分式化为最简形式,再代入求值.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (ab)2=a2b2 | D. | (-ab2)2=-a2b4 |
10.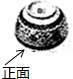 如图,将一只青花碗放在水平桌面上,它的左视图是( )
如图,将一只青花碗放在水平桌面上,它的左视图是( )
 如图,将一只青花碗放在水平桌面上,它的左视图是( )
如图,将一只青花碗放在水平桌面上,它的左视图是( )| A. |  | B. | 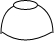 | C. |  | D. | 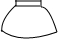 |
14.下列乘法中,不能运用平方差公式进行计算的是( )
| A. | (x+a)(x-a) | B. | (a+b)(-a-b) | C. | (-x-b)(x-b) | D. | (b+m) (m-b) |
12.如果一个△ABC的两个内角A,B分别是67°,46°,则该三角形( )
| A. | 不是轴对称图形 | |
| B. | 是轴对称图形,且有三条对称轴 | |
| C. | 是轴对称图形,且对称轴是AC边上的高所在的直线 | |
| D. | 以上答案都不对 |
 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.