题目内容
1.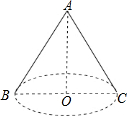 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,则圆锥的侧面展开图扇形的圆心角度约为( )| A. | 127° | B. | 180° | C. | 201° | D. | 255° |
分析 由△ABC是直角三角形,而AB=AC,得出△ABC是等腰直角三角形,设圆锥底面圆的半径OB=r,则母线AB=AC=$\sqrt{2}$r,设所求圆心角度数为n,根据圆锥的侧面展开图中扇形的弧长等于圆锥底面的周长列出关于n的方程,解方程即可.
解答 解:∵圆锥的轴截面(过圆锥顶点和底面圆心的截面)△ABC是直角三角形,
∴△ABC是等腰直角三角形,
设圆锥底面圆的半径OB=r,则母线AB=AC=$\sqrt{2}$r,
设所求圆心角度数为n,则$\frac{nπ•\sqrt{2}r}{180}$=2πr,
解得n=180$\sqrt{2}$≈255.
故选D.
点评 本题考查了圆锥的计算,理解圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.由圆锥的轴截面△ABC是直角三角形得出△ABC是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边长为39,那么较大的三角形的面积为( )
| A. | 90 | B. | 180 | C. | 270 | D. | 540 |
16.某校九(1)班进行了一次体育测试,期中第一小组的成绩分别是(单位:分)30,25,29,28,28,30,29,28,20,28,27,30.这组数据的众数和中位数分别是( )
| A. | 28分,28分 | B. | 30分,28分 | C. | 28分,27.5分 | D. | 30分,27.5分 |
13.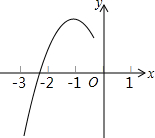 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
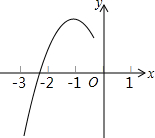 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
| A. | ②③ | B. | ①③ | C. | ①②③ | D. | ①②④ |
11. 下图中的几何体的左视图是( )
下图中的几何体的左视图是( )
 下图中的几何体的左视图是( )
下图中的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
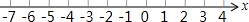 解不等式组:$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$,并把解集在数轴上表示出来.