��Ŀ����
9�������������������и�ʽ����1��$\sqrt{{4}^{2}+{3}^{2}}$=5��
��2��$\sqrt{{44}^{2}+{33}^{2}}$=55��
��3��$\sqrt{{444}^{2}+{333}^{2}}$=555��
��4��$\sqrt{{4444}^{2}+{3333}^{2}}$=5555��
�Բ���$\sqrt{\underset{\underbrace{44��{4}^{2}}}{2015��}+\underset{\underbrace{33��{3}^{2}}}{2015��}}$�Ľ��Ϊ$\underset{\underbrace{55��5}}{2015��5}$��
���� ���ȸ������Ŀ��������㷽�����ֱ����$\sqrt{{4}^{2}+{3}^{2}}$��$\sqrt{{44}^{2}+{33}^{2}}$��$\sqrt{{444}^{2}+{333}^{2}}$��$\sqrt{{4444}^{2}+{3333}^{2}}$��ֵ���Ƕ��٣�Ȼ��������õĽ���ܽ�����ɣ�����Ӧ���ܽ�Ĺ��ɣ�����$\sqrt{\underset{\underbrace{44��{4}^{2}}}{2015��}+\underset{\underbrace{33��{3}^{2}}}{2015��}}$�Ľ��Ϊ���ټ��ɣ�
��� �⣺���ݷ������ɵ�
��1��$\sqrt{{4}^{2}+{3}^{2}}$=5��
��2��$\sqrt{{44}^{2}+{33}^{2}}$=55��
��3��$\sqrt{{444}^{2}+{333}^{2}}$=555��
��4��$\sqrt{{4444}^{2}+{3333}^{2}}$=5555��
����$\sqrt{\underset{\underbrace{44��{4}^{2}}}{2015��}+\underset{\underbrace{33��{3}^{2}}}{2015��}}$�Ľ��Ϊ��$\underset{\underbrace{55��5}}{2015��5}$��
�ʴ�Ϊ��5��55��555��5555��$\underset{\underbrace{55��5}}{2015��5}$��
���� ������Ҫ�����˼�����-���Ŀ������⣬�Լ�̽Ѱ���������Ӧ�ã�Ҫ�������գ�ע��۲��ܽ�����ɣ�������ȷ��Ӧ�ù��ɣ�

 ��������ϵ�д�
��������ϵ�д�| A�� | -2 | B�� | 0 | C�� | -$\frac{5}{2}$ | D�� | 2 |
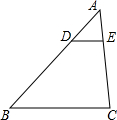 ��ͼ���ڡ�ABC�У�DE��BC��$\frac{AD}{DB}=\frac{1}{2}$�������н�������ȷ���ǣ�������
��ͼ���ڡ�ABC�У�DE��BC��$\frac{AD}{DB}=\frac{1}{2}$�������н�������ȷ���ǣ�������| A�� | $\frac{AE}{EC}=\frac{1}{2}$ | B�� | $\frac{DE}{BC}=\frac{1}{2}$ | ||
| C�� | $\frac{��ADE���ܳ�}{��ABC���ܳ�}=\frac{1}{2}$ | D�� | $\frac{��ADE�����}{��ABC�����}=\frac{1}{3}$ |