题目内容
14.用计算器探索:(1)$\sqrt{{1}^{3}}$=1.
(2)$\sqrt{{1}^{3}+{2}^{3}}$=3.
(3)$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}}$=6.
(4)$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}+{4}^{3}}$=10.
…
(5)通过观察,我们发现:$\sqrt{{1}^{3}+{2}^{3}+…+{n}^{3}}$=$\frac{1}{2}n(n+1)$(n为正整数).
分析 首先根据数的开方的运算方法,分别求出$\sqrt{{1}^{3}}$、$\sqrt{{1}^{3}+{2}^{3}}$、$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}}$、$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}+{4}^{3}}$的值各是多少;然后根据所得的结果总结出规律,并能应用总结的规律,求出$\sqrt{{1}^{3}+{2}^{3}+…+{n}^{3}}$的值是多少即可.
解答 解:(1)$\sqrt{{1}^{3}}$=1.
(2)$\sqrt{{1}^{3}+{2}^{3}}$=3.
(3)$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}}$=6.
(4)$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}+{4}^{3}}$=10.
…
∵1=1,
3=1+2,
6=1+2+3,
10=1+2+3+4,
∴$\sqrt{{1}^{3}+{2}^{3}+…+{n}^{3}}$=1+2+3+…+n=$\frac{1}{2}n(n+1)$(n为正整数).
故答案为:1、3、6、10、$\frac{1}{2}n(n+1)$.
点评 此题主要考查了计算器-数的开方问题,以及探寻规律问题的应用,要熟练掌握,注意观察总结出规律,并能正确的应用规律.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,AB∥CD,AB=$\frac{2\sqrt{3}}{3}$,AB与CD间的距离是3$\sqrt{3}$,求AC,BD和CD的长.
如图,AB∥CD,AB=$\frac{2\sqrt{3}}{3}$,AB与CD间的距离是3$\sqrt{3}$,求AC,BD和CD的长.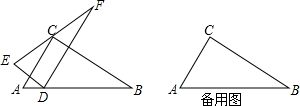
 当a为何值时,四边形PABN的周长最小,并求出最小值.
当a为何值时,四边形PABN的周长最小,并求出最小值.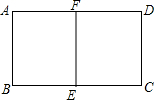 如图,有-张矩形纸片,将其对折后的矩形与原来的矩形形状相同,则原矩形长与宽的比是多少?
如图,有-张矩形纸片,将其对折后的矩形与原来的矩形形状相同,则原矩形长与宽的比是多少?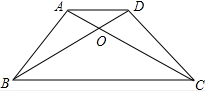 如图所示.老师上完“三角形相似的判定”一课后,出了如下一道思考题:在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,试问:△AOB和△DOC是否相似?
如图所示.老师上完“三角形相似的判定”一课后,出了如下一道思考题:在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,试问:△AOB和△DOC是否相似? 如图,每个小方格的边长都为1,在图中画出以格点为端点,长度为10个单位长度的线段.
如图,每个小方格的边长都为1,在图中画出以格点为端点,长度为10个单位长度的线段.