题目内容
17.设k<0,当二次函数y=$\frac{1}{2}{x^2}+kx+k-\frac{1}{2}$的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.分析 依据二次函数y=$\frac{1}{2}{x^2}+kx+k-\frac{1}{2}$的图象与x轴的两个交点A、B间的距离为4,列方程求出k即可.
解答 解:设二次函数y=$\frac{1}{2}{x^2}+kx+k-\frac{1}{2}$的图象与x轴的两个交点A、B的横坐标分别为x1、x2,
x1+x2=-2k,x1x2=2k-1,
∵|x1x1x1-x2|=$\sqrt{({x}_{1}-{x}_{2})^{2}}$=4.
∴(x1-x2)2=16,
变形为:(x1+x2)2-4x1•x2=16,
∴4k2-4(2k-1)=16,
整理得:k2-2k-3=0,
解得:k1=3,k2=-1,
∵k<0,
∴k=-1,
∴y=$\frac{1}{2}$x2-x-$\frac{3}{2}$;
故答案为:y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.
点评 本题主要考查了抛物线与x轴的交点,熟悉二次函数与一元二次方程的关系和坐标轴上两点距离公式|x1-x2|,并熟练运用.

练习册系列答案
相关题目
8.如果2x+1是多项式6x2+mx-5的一个因式,则m的值是( )
| A. | 6 | B. | -6 | C. | 7 | D. | -7 |
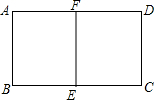 如图,有-张矩形纸片,将其对折后的矩形与原来的矩形形状相同,则原矩形长与宽的比是多少?
如图,有-张矩形纸片,将其对折后的矩形与原来的矩形形状相同,则原矩形长与宽的比是多少?