题目内容
1.(1)若5a+1和a-19是数m的平方根,求m的值.(2)已知$\sqrt{1-3a}$和|8b-3|互为相反数,求(ab)2-27的值.
分析 (1)根据正数的平方根互为相反数列方程求出a的值,然后求出一个平方根,再平方计算即可;
(2)根据互为相反数的两个数的和等于0列出方程,再根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:(1)∵5a+1和a-19是数m的平方根,
∴5a+1+a-19=0,
解得a=3,
所以,5a+1=5×3+1=16,
∴m=162=256,
或:5a+1=a-19,
解得a=-5,
所以,5a+1=5×(-5)+1=24,
∴m=242=576,
综上所述,m的值为256或576;
(2)∵$\sqrt{1-3a}$和|8b-3|互为相反数,
∴$\sqrt{1-3a}$+|8b-3|=0,
∴1-3a=0,8b-3=0,
解得a=$\frac{1}{3}$,b=$\frac{3}{8}$,
所以,(ab)2-27=($\frac{1}{3}$×$\frac{3}{8}$)2-27=$\frac{1}{64}$-27=-26$\frac{63}{64}$.
点评 本题考查了平方根,非负数的性质,几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若$\root{3}{0.3670}$=0.7160,$\root{3}{3.670}$=1.542,则$\root{3}{367}$=7.16,$\root{3}{-3670}$=-15.42.
6.出租车司机小王某天下午营运全是在东西走向的汶河大道上进行的,如果规定向东为正,向西为负,这天下午他的行车里程(单位:千米)如下表所示:
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.1升/千米,这天下午小王共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | 第十一次 |
| +15 | -2 | +5 | -1 | +10 | -3 | -2 | +12 | +4 | -5 | +6 |
(2)若汽车耗油量为0.1升/千米,这天下午小王共耗油多少升?
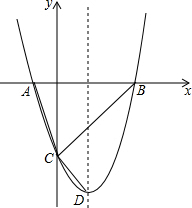 如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.
如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.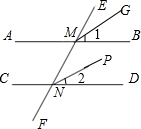 如图,直线AB和直线CD被直线EF所截,∠BMN=∠DNF,∠1=∠2,那么MG与NP平行吗?请说明理由.
如图,直线AB和直线CD被直线EF所截,∠BMN=∠DNF,∠1=∠2,那么MG与NP平行吗?请说明理由.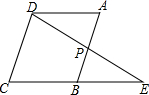 如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.
如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.