题目内容
6. 已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:
已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,
从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有多少组可能?请写出所有可能的组合;并选择其中一组加以证明.
分析 根据平行四边形的判定来进行选择.选择①与②:根据AAS证明△AOB≌△COD,根据全等三角形的性质得到AB=CD,根据一组对边平行且相等的四边形是平行四边形即可证明.
解答 解:共有6组可能:①②;①③;①④;①⑤;②⑤;④⑤.
选择①与②:∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
在△AOB与△COD中,
$\left\{\begin{array}{l}{∠ABO=∠CDO}\\{∠BAO=∠DCO}\\{OA=OC}\end{array}\right.$,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD为平行四边形.
点评 本题考查了平行四边形的判定,熟练掌握判定定理是解题的关键.平行四边形共有五种判定方法,记忆时要注意技巧;这五种方法中,一种与对角线有关,一种与对角有关,其他三种与边有关.

练习册系列答案
相关题目
14.将点A(-4,-2)向右平移5的单位长度得到点B,则点B的所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
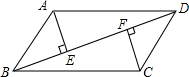 如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.
如图,BD是?ABCD的一条对角线,AE⊥BD,CF⊥BD,试猜想AE和CF的数量关系,并对你的猜想进行证明.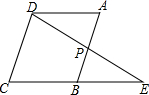 如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.
如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于点E,求证:BE=AD.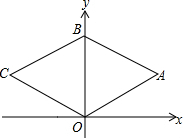 如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.
如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.