题目内容
16.正六边形的周长为6,则它的面积为( )| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
分析 首先根据题意画出图形,即可得△OBC是等边三角形,又由正六边形ABCDEF的周长为6,即可求得BC的长,继而求得△OBC的面积,则可求得该六边形的面积.
解答 解:如图,连接OB,OC,过O作OM⊥BC于M,
∴∠BOC=$\frac{1}{2}$×360°=60°,
∵OB=OC,
∴△OBC是等边三角形,
∵正六边形ABCDEF的周长为6,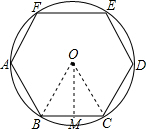
∴BC=6÷6=1,
∴OB=BC=1,
∴BM=$\frac{1}{2}$BC=$\frac{1}{2}$,
∴OM=$\sqrt{O{B}^{2}-B{M}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴S△OBC=$\frac{1}{2}$×BC×OM=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
∴该六边形的面积为:$\frac{\sqrt{3}}{4}$×6=$\frac{3\sqrt{3}}{2}$.
故选:C.
点评 此题考查了圆的内接六边形的性质与等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4.已知⊙O的半径为6cm,点O到直线l的距离为5cm,则直线l与⊙O( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 相切或相交 |
1.A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )
| A. | 4小时 | B. | 4.5小时 | C. | 5小时 | D. | 4小时或5小时 |
6.若关于x的不等式$\left\{\begin{array}{l}{x-m≤0}\\{5-2x<1}\end{array}\right.$共有2个整数解,则m的取值范围( )
| A. | 4<m<5 | B. | 4<m≤5 | C. | 4≤m≤5 | D. | 4≤m<5 |
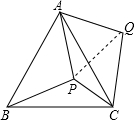 P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.
P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2. 如图,矩形RFGD的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,且DE=2EF,△ABC中,边BC的长度为12cm,高AH为8cm,求矩形DEFG的面积.
如图,矩形RFGD的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,且DE=2EF,△ABC中,边BC的长度为12cm,高AH为8cm,求矩形DEFG的面积.