题目内容
1.A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )| A. | 4小时 | B. | 4.5小时 | C. | 5小时 | D. | 4小时或5小时 |
分析 设当两车相距100千米时,甲车行驶的时间为x小时,根据路程=速度×时间结合两车相距100千米即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:设当两车相距100千米时,甲车行驶的时间为x小时,
根据题意得:900-(110+90)x=100或(110+90)x-900=100,
解得:x=4或x=5.
故选D.
点评 本题考查了一元一次方程的应用,根据数量关系路程=速度×时间,列出一元一次方程是解题的关键.

练习册系列答案
相关题目
16.正六边形的周长为6,则它的面积为( )
| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
13.计算(-$\frac{1}{3}$)-2的值,正确的是( )
| A. | $\frac{1}{9}$ | B. | -$\frac{1}{9}$ | C. | 9 | D. | -9 |
10. 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )| A. | 1.5小时 | B. | 1.8小时 | C. | 2小时 | D. | 2.5小时 |
11.方程x2=4的解是( )
| A. | x=2 | B. | x=-2 | C. | x1=1,x2=4 | D. | x1=2,x2=-2 |
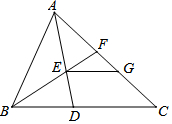 如图,△ABC中,∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG∥BC交AC于点G.
如图,△ABC中,∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG∥BC交AC于点G. 如图,已知:?ABCD的对角线AC,BD相交于点O,EF过O,AD=8,AB=6,OE=4,则四边形ABFE的周长是多少?
如图,已知:?ABCD的对角线AC,BD相交于点O,EF过O,AD=8,AB=6,OE=4,则四边形ABFE的周长是多少?