题目内容
8.下列各式中,不能用平方差公式分解的是( )| A. | -a2+b2 | B. | -x2-y2 | C. | 49x2y2-z2 | D. | 16m4-25n2 |
分析 利用平方差公式的结构特征判断即可.
解答 解:-x2-y2不能利用平方差公式分解,
故选B
点评 此题考查了因式分解-运用公式法,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | (+$\frac{1}{2}$)+(+$\frac{1}{3}$)=$\frac{1}{5}$ | B. | (+$\frac{1}{2}$)+(-$\frac{1}{3}$)=-$\frac{1}{6}$ | C. | (-$\frac{1}{2}$)+(+$\frac{1}{3}$)=$\frac{1}{6}$ | D. | (-$\frac{1}{2}$)+(+$\frac{1}{3}$)=-$\frac{1}{6}$ |
16.下列判定直角三角形全等的方法,不正确的是( )
| A. | 两条直角边对应相等 | B. | 斜边和一锐角对应相等 | ||
| C. | 斜边和一直角边对应相等 | D. | 两个直角三角形的面积相等 |
3.下列各式中,最简二次根式是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{26}$ | C. | $\sqrt{0.5}$ | D. | $\frac{\sqrt{2}}{\sqrt{3}}$ |
13.以下列各组数为三角形的三边的长,能组成一个直角三角形的是( )
| A. | 3、4、6 | B. | 24、10、26 | C. | 8、12、15 | D. | 7、9、14 |
18.若m+n=0,则m,n的取值一定是( )
| A. | 都是0 | B. | 至少有一个等于0 | C. | 互为相反数 | D. | m是正数,n是负数 |
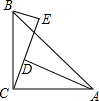 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.