题目内容
在△ABC中,AB=
,BC=1,∠ABC=30°,以AB为边作等边△ABD,连接CD,求线段CD的长.
| 3 |
考点:解直角三角形
专题:计算题
分析:分类讨论:当△ABC和△ABD在AB的同侧,由于△ABD为等边三角形,则∠ABD=60°,而∠ABC=30°,所以BE平分∠ABD,于是可判断点C为△ABC的外心,则CD=BC=1;
当△ABC和△ABD在AB的异侧,即△ABD′,在Rt△ABE中,∠ABE=30°,AB=
,根据含30度的直角三角形三边的关系得到AE=
AB=
,BE=
AE=
,则CE=BE-BC=
,于是有CD′=BE+CE=
+
=2.
当△ABC和△ABD在AB的异侧,即△ABD′,在Rt△ABE中,∠ABE=30°,AB=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:如图,
当△ABC和△ABD在AB的同侧,
∵△ABD为等边三角形,
∴∠ABD=60°,
∵∠ABC=30°,
∴BE平分∠ABD,
∴BE垂直平分AD,
∴点C为△ABC的外心,
∴CD=BC=1;
当△ABC和△ABD在AB的异侧,即△ABD′,
在Rt△ABE中,∠ABE=30°,AB=
,
∴AE=
AB=
,
∴BE=
AE=
,
∴CE=BE-BC=
∴CD′=BE+CE=
+
=2,
即线段CD的长为1或2.

当△ABC和△ABD在AB的同侧,
∵△ABD为等边三角形,
∴∠ABD=60°,
∵∠ABC=30°,
∴BE平分∠ABD,
∴BE垂直平分AD,
∴点C为△ABC的外心,
∴CD=BC=1;
当△ABC和△ABD在AB的异侧,即△ABD′,
在Rt△ABE中,∠ABE=30°,AB=
| 3 |
∴AE=
| 1 |
| 2 |
| ||
| 2 |
∴BE=
| 3 |
| 3 |
| 2 |
∴CE=BE-BC=
| 1 |
| 2 |
∴CD′=BE+CE=
| 1 |
| 2 |
| 3 |
| 2 |
即线段CD的长为1或2.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
等式
=
成立的条件是( )
| ||
|
|
| A、0≤x<1 | B、x≥0 |
| C、x<1 | D、x≥0或x<1 |
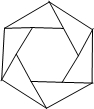 如图,把面积为a的正六边形的各边按同一方向延长,使延长的线段与原六边形的边长相等,顺次连接这六条线段的外端点可以得到一个新的正六边形,重复上述过程,经过6次后,所得正六边形的面积是( )
如图,把面积为a的正六边形的各边按同一方向延长,使延长的线段与原六边形的边长相等,顺次连接这六条线段的外端点可以得到一个新的正六边形,重复上述过程,经过6次后,所得正六边形的面积是( )| A、243a | ||
| B、729a | ||
| C、2187a | ||
D、243
|
已知x2-(m-1)x-(2m-2)=0两根之和等于两根之积,则m的值为( )
| A、1 | B、-1 | C、2 | D、-2 |
 如图,在平行四边形ABCD中,AB=4,BC=2,∠A=60°.
如图,在平行四边形ABCD中,AB=4,BC=2,∠A=60°.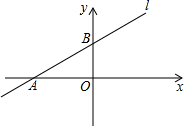 如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的
如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的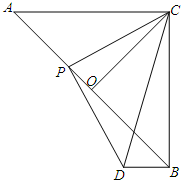 如图,等腰Rt△ABC的直角边长为2
如图,等腰Rt△ABC的直角边长为2