题目内容

1．已知一个n棱柱共有12条棱，那么这个n棱柱共有8个顶点．

分析 根据n棱柱有n+2面，3n条棱，2n个顶点求解即可．

解答 解：根据题意得：3n=12．
解得：n=4．
2×4=8．
故答案为：8．

点评 本题主要考查的是认识立体图形，明确n棱柱有有n+2面，3n条棱，2n个顶点是解题的关键．

练习册系列答案
相关题目
11．解分式方程：$\frac{x}{2x-3}$-$\frac{1}{x-5}$=$\frac{1}{2}$．
12．满足下列条件的三角形中，不是直角三角形的是（　　）
A．三内角的度数之比为1：2：3B．三内角的度数之比为3：4：5
C．三边长之比为3：4：5D．三边长的平方之比为1：2：3
9．已知一次函数y=（m+2）x+2-n，求：
（1）y随x的增大而增大，m的取值范围；
（2）函数的图象与y轴的交点在x轴的下方时，m，n的取值范围；
（3）m，n为何值时图象与坐标轴交于原点；
（4）函数的图象经过第一、二、三象限，m，n的取值范围．
16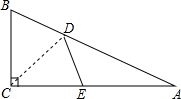．如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的E处．若∠A=23°，则∠BDC等于（　　）
A．46°B．60°C．68°D．77°
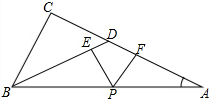6．已知，如图，在△ABC中，∠C=90°，点D、P分别在边AC、AB上，且BD=AD，PE⊥BD，PF⊥AD，垂足分别为点E、F．
（1）当∠A=30°时，求证：PE+PF=BC；
（2）当A≠30°（∠A＜∠ABC）时，试问以上结论是否依然正确？如果正确，请加以证明；如果不正确，请说明理由．
13．抛物线y=-x2+（b+1）x-3的顶点在y轴上，则b的值为-1．
10．用下面方法确定$\sqrt{2}$的前面的几个小数位上的字．
阅读理解：
我们知道，正方形面积越大，其边长也越大，即如果两个正方形的面积分别为a、b，且a＜b，那么$\sqrt{a}＜\sqrt{b}$
因为12＜2＜22，所以1＜$\sqrt{2}$＜2，可知$\sqrt{2}$的整数部分是1
（1）取$\frac{1+2}{2}$=1.5，由1.52=2.25＞2，得1＜$\sqrt{2}$＜1.5
（2）取$\frac{1+1.5}{2}=1.25，由1，2{5}^{2}$＜1.6＜2，得1.25＜$\sqrt{2}$＜1.5
操作实践；
继续像（1）、（2）那样取值和比较，确定$\sqrt{2}$的十分位和百分位上的数字．
11．△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若添加条件∠B=∠C，则可用（　　）
A．SSSB．AASC．HLD．不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网