题目内容
6.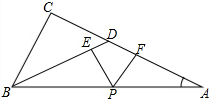 已知,如图,在△ABC中,∠C=90°,点D、P分别在边AC、AB上,且BD=AD,PE⊥BD,PF⊥AD,垂足分别为点E、F.
已知,如图,在△ABC中,∠C=90°,点D、P分别在边AC、AB上,且BD=AD,PE⊥BD,PF⊥AD,垂足分别为点E、F.(1)当∠A=30°时,求证:PE+PF=BC;
(2)当A≠30°(∠A<∠ABC)时,试问以上结论是否依然正确?如果正确,请加以证明;如果不正确,请说明理由.
分析 (1)根据直角三角形的性质得到PA=2PF,PB=2PE,证明结论;
(2)运用三角形的面积公式得到△ABD的面积=$\frac{1}{2}$×AD×(PE+PF),△ABD的面积=$\frac{1}{2}$×AD×BC,得到答案.
解答 证明:(1)∵∠A=30°,PF⊥AD,
∴PA=2PF,
同理,PB=2PE,
∴BA=2(PE+PF),
∵∠A=30°,∠C=90°,
∴BA=2BC,
∴PE+PF=BC;
(2)成立,
连接DP,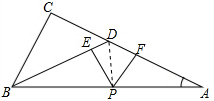
△PDA的面积=$\frac{1}{2}$×AD×PF,
△PDB的面积=$\frac{1}{2}$×BD×PE,又BD=AD,
∴△ABD的面积=$\frac{1}{2}$×AD×(PE+PF),又△ABD的面积=$\frac{1}{2}$×AD×BC,
∴PE+PF=BC.
点评 本题考查的是三角形的面积的计算和直角三角形的性质,掌握在直角三角形中,30°所对的直角边是斜边的一半是解题的关键,注意三角形的面积公式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.-(-9)的相反数是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
11.抛物线y=(x+1)2-2的对称轴是( )
| A. | 直线x=1 | B. | 直线x=3 | C. | 直线x=-1 | D. | 直线x=-3 |
18.在时刻8:40,时钟上的时针和分针之间的夹角为( )
| A. | 15° | B. | 20° | C. | 25° | D. | 10° |
15.某商品按进价的100%加价出售,经过一段时间,商家为减少库存,决定以7折销售,这时每件商品( )
| A. | 赚40% | B. | 赔30% | C. | 赔40% | D. | 不赔不赚 |
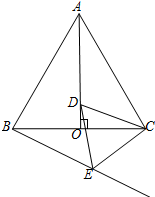 如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.
如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.