题目内容
16.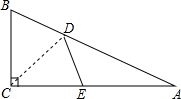 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )| A. | 46° | B. | 60° | C. | 68° | D. | 77° |
分析 在△ABC中,先求得∠B=67°,由翻折的性质可知∠DEC=67°,由∠A+∠ADE=∠DEC可求得∠ADE=44°,然后根据∠BDC=$\frac{1}{2}(180°-∠ADE)$求解即可.
解答 解:∵∠A+∠B=90°,
∴∠B=90°-23°=67°.
由翻折的性质可知:∠B=∠DEC=67°,∠BDC=∠EDC.
∵∠A+∠ADE=∠DEC,
∴∠EDA=67°-23°=44°.
∴∠BDC=$\frac{1}{2}(180°-∠ADE)$=$\frac{1}{2}×(180°-44°)$=68°.
故选:C.
点评 本题主要考查的是翻折的性质,由三角形外角的性质求得∠EDA的度数是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.一元二次方程2x(3x-2)=(x-1)(3x-2)的解是( )
| A. | x=-1 | B. | x=$\frac{2}{3}$ | C. | x1=$\frac{2}{3}$,x2=0 | D. | x1=$\frac{2}{3}$,x2=-1 |
4. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.抛物线y=-x2+x+2与y轴的交点坐标是( )
| A. | (1,2) | B. | (0,-1) | C. | (0,1) | D. | (0,2) |
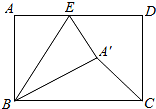 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD 的平分线上时,CA′的长为多少?
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD 的平分线上时,CA′的长为多少?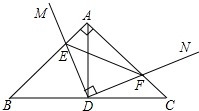 如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10.
如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10. 如图,∠DAC=∠BAC-∠BAD,∠BDC=∠BDA+∠ADC.
如图,∠DAC=∠BAC-∠BAD,∠BDC=∠BDA+∠ADC.