题目内容
9.已知一次函数y=(m+2)x+2-n,求:(1)y随x的增大而增大,m的取值范围;
(2)函数的图象与y轴的交点在x轴的下方时,m,n的取值范围;
(3)m,n为何值时图象与坐标轴交于原点;
(4)函数的图象经过第一、二、三象限,m,n的取值范围.
分析 (1)根据一次函数的性质可知:m+2>0;
(2)根据一次函数的性质进行解答即可;
(3)把x=0,y=0代入解析式解答即可;
(4)根据函数的图象经过第一、二、三象限列出不等式解答即可.
解答 解:(1)∵函数y的值随x值的增大而增大
∴m+2>0,
∴m>-2;
(2)∵函数的图象与y轴的交点在x轴的下方,
∴2-n<0,m+2≠0
∴n>2,m≠-2;
(3)∵函数的图象与坐标轴交于原点,
∴2-n=0,m+2≠0,
∴n=2,m≠-2,
(4)∵函数的图象经过第一、二、三象限,
∴m+2>0,2-n>0,
∴n<2,m>-2.
点评 本题主要考查一次函数的图象与系数的关系,当x的系数大于0时,函数y随自变量x的增大而增大.

练习册系列答案
相关题目
17.-(-9)的相反数是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
4. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.在时刻8:40,时钟上的时针和分针之间的夹角为( )
| A. | 15° | B. | 20° | C. | 25° | D. | 10° |
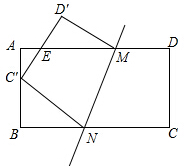 如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.
如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.