题目内容
19. 如图,△ABC中,CD⊥AB于D,且E是AC的中点.若AD=6,DE=5,则CD的长等于( )
如图,△ABC中,CD⊥AB于D,且E是AC的中点.若AD=6,DE=5,则CD的长等于( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 先根据直角三角形的性质求出AC的长,再根据勾股定理即可得出结论.
解答 解:∵△ABC中,CD⊥AB于D,
∴∠ADC=90°.
∵E是AC的中点,DE=5,
∴AC=2DE=10.
∵AD=6,
∴CD=$\sqrt{{AC}^{2}-{AD}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8.
故选D.
点评 本题考查的是直角三角形斜边上的中线,熟知在直角三角形中,斜边上的中线等于斜边的一半是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.李想大学毕业后与同学进行自主创业,计划购进A、B两种新型节能台灯100盏,这两种台灯的进价、售价如表所示:
(1)设A型台灯购进x台,共获利W元,写出W与x的函数关系式;
(2)若规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能在销售完这批台灯时获利最多?此时W为多少?
(1)设A型台灯购进x台,共获利W元,写出W与x的函数关系式;
(2)若规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能在销售完这批台灯时获利最多?此时W为多少?
| 类型 | 进价(元/盏) | 售价(元/盏) |
| A型 | 40 | 60 |
| B型 | 50 | 80 |
14.某服装店销售每件进价为200元、170元的A、B两种品牌的上衣,下列是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种品牌上衣的销售单价;
(2)若超市准备用不多余5400元的金额再采购这两种品牌的上衣共30件,则A品牌的上衣最多能采购多少件?
| 销售时段 | 销售数量 | 销售收入 | |
| A品牌 | B品牌 | ||
| 第一周 | 3件 | 5件 | 1800元 |
| 第二周 | 4件 | 10件 | 3100元 |
(1)求A、B两种品牌上衣的销售单价;
(2)若超市准备用不多余5400元的金额再采购这两种品牌的上衣共30件,则A品牌的上衣最多能采购多少件?
4.用计算器求得$\sqrt{3}$+$\root{3}{3}$的结果(保留4个有效数字)是( )
| A. | 3.1742 | B. | 3.174 | C. | 3.175 | D. | 3.1743 |
11.下列长度的三条线段能组成三角形的是( )
| A. | 5,6,10 | B. | 5,6,11 | C. | 3,4,8 | D. | 4a,4a,8a(a>0) |
8.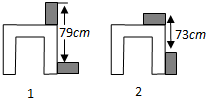 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )| A. | 73cm | B. | 74cm | C. | 75cm | D. | 76cm |
9.下列调查中,适合普查方法的是( )
| A. | 了解一批灯泡的使用寿命 | |
| B. | 了解某班学生对“社会主义核心价值观”的知晓率 | |
| C. | 了解全国中学生体重情况 | |
| D. | 了解北京电视台《红绿灯》栏目的收视率 |
 如图,正方形ABCD中,△ADE经顺时针旋转后与△ABF重合.
如图,正方形ABCD中,△ADE经顺时针旋转后与△ABF重合.