题目内容
7.李想大学毕业后与同学进行自主创业,计划购进A、B两种新型节能台灯100盏,这两种台灯的进价、售价如表所示:(1)设A型台灯购进x台,共获利W元,写出W与x的函数关系式;
(2)若规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能在销售完这批台灯时获利最多?此时W为多少?
| 类型 | 进价(元/盏) | 售价(元/盏) |
| A型 | 40 | 60 |
| B型 | 50 | 80 |
分析 (1)根据题直接意列函数关系即可;
(2)根据一次函数的增减性求解即可.
解答 解:(1)W=(60-40)x+(80-50)(100-x),
=-10x+3000;
(2)100-x≤3x,
x≥25 (上限不要求)
∵W随x的增大而减小,
∴x=25时,W最大=-10×25+3000=2750,
∴购进A型台灯25盏,B型台灯75盏时,销售完这批台灯时获利最多,此时利润为2750元.
点评 本题考查了一次函数的应用,主要利用了一次函数的增减性,(2)题中理清题目数量关系并列式求出x的取值范围是解题的关键.

练习册系列答案
相关题目
17.因式分解x2-9y2的正确结果是( )
| A. | (x+9y)(x-9y) | B. | (x+3y)(x-3y) | C. | (x-3y)2 | D. | (x-9y)2 |
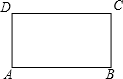 已知:如图,长方形ABCD中,AB=8,BC=6,平移长方形ABCD到长方形A1B1C1D1,使得与原长方形ABCD重合部分的面积是12,请你写出一种可行的平移方案将长方形ABCD沿着AB边向右平移6个单位,得到长方形A1B1C1D1(一种即可).
已知:如图,长方形ABCD中,AB=8,BC=6,平移长方形ABCD到长方形A1B1C1D1,使得与原长方形ABCD重合部分的面积是12,请你写出一种可行的平移方案将长方形ABCD沿着AB边向右平移6个单位,得到长方形A1B1C1D1(一种即可). 如图,在△ABC中,AB=AC,点D是BC的中点,DE⊥AC于点E,DG⊥AB于点G,EK⊥AB于点K,GH⊥AC于点H、EK和GH相交于点F.
如图,在△ABC中,AB=AC,点D是BC的中点,DE⊥AC于点E,DG⊥AB于点G,EK⊥AB于点K,GH⊥AC于点H、EK和GH相交于点F.
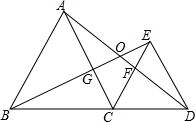 如图,△ABC和△ECD都是等边三角形,B、C、D三点在一条直线上,AD与BE相交于点O,AD与CE相交于点F,AC与BE相交于点G.
如图,△ABC和△ECD都是等边三角形,B、C、D三点在一条直线上,AD与BE相交于点O,AD与CE相交于点F,AC与BE相交于点G. 如图,△ABC中,CD⊥AB于D,且E是AC的中点.若AD=6,DE=5,则CD的长等于( )
如图,△ABC中,CD⊥AB于D,且E是AC的中点.若AD=6,DE=5,则CD的长等于( )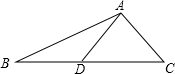 如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC=52度.
如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC=52度.