题目内容
2.已知一次函数y=kx+5和y=k′x+1,假设k>0且k′<0,则这两个一次函数的图象的交点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据一次函数图象与系数的关系大致画出两个一次函数的图象,观察函数图象即可得出结论.
解答 解:∵一次函数y=kx+5中,k>0,5>0,
∴一次函数y=kx+5的图象经过第一、二、三象限;
∵一次函数y=k′x+1中,k′<0,1>0,
∴一次函数y=k′x+1的图象经过第一、二、四象限.
大致画出两个一次函数的图象,如图所示,
观察函数图象可知:这两个一次函数的图象的交点在第二象限.
故选B.
点评 本题考查了一次函数图象与系数的关系以及两条直线相交或平行问题,大致画出函数图象,利用数形结合解决问题是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列计算正确的是( )
| A. | $\sqrt{6}÷(\sqrt{3}-\sqrt{2})=\sqrt{2}-\sqrt{3}$ | B. | $\sqrt{(-9)×(-25)}=\sqrt{-9}×\sqrt{-25}=(-3)×(-5)=15$ | ||
| C. | $\sqrt{2}(\sqrt{3}+\sqrt{2})=\sqrt{10}$ | D. | $\sqrt{{{13}^2}-{{12}^2}}=\sqrt{(13+12)×(13-12)}=5$ |
11.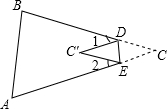 如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
 如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )| A. | 33° | B. | 34° | C. | 31° | D. | 32° |
 如图,在△ABC中,∠ACB=90°,将△ACD沿CD折叠,使点A恰好落在BC边上的点E处.若∠B=25°,则∠BDE=40度.
如图,在△ABC中,∠ACB=90°,将△ACD沿CD折叠,使点A恰好落在BC边上的点E处.若∠B=25°,则∠BDE=40度.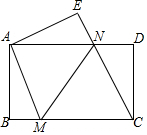 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N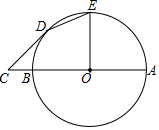 已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2
已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2 如图,小红用一张长方形纸片ABCD进行折纸,已知纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求此时EC的长?
如图,小红用一张长方形纸片ABCD进行折纸,已知纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求此时EC的长?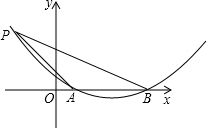 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求:
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求: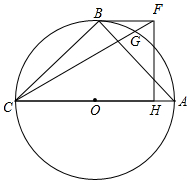 如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.