题目内容
11．
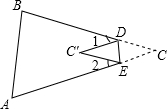如图，将△ABC纸片的一角折叠，使点C落在△ABC内一点C′上，若∠1=30°，∠2=36°，则∠C的度数是（ ）| A． | 33° | B． | 34° | C． | 31° | D． | 32° |
分析 根据折叠的性质可以得到，∠C′DE=∠CDE，∠C′ED=∠CED，根据平角定义得出∠1+∠C′DC=180°，∠2+∠C′EC=180°，求出∠C′DC+∠C′EC，在四边形C′DCE中，根据内角和定理求出即可；
解答 解：∵△C′DE是由△CDE折叠而成，
∴∠C=∠C′，∠C′DE=∠CDE，∠C′ED=∠CED，
又∠1+∠C′DC=180°，∠2+∠C′EC=180°，
∴∠C′DC+∠C′EC=360°-（∠1+∠2）=294°，
又四边形C′DCE的内角和为360°，
∴∠C′+∠C=66°，
∴∠C=33°．
故选A．
点评 本题考查的是三角形内角和定理及平角的性质，解答此题的关键是熟知三角形的内角和是180°．
练习册系列答案
名校课堂系列答案
相关题目
2．已知一次函数y=kx+5和y=k′x+1，假设k＞0且k′＜0，则这两个一次函数的图象的交点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．如果方程x2+mx-1=0的两个实根互为相反数，那么m的值为（ ）
| A． | 0 | B． | -1 | C． | 1 | D． | ±1 |
如图，平行四边形ABCO中，AO=1，AB=3，点C在x轴的负半轴上，将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF，AD经过点O，点F恰好落在x轴上，若点D在反比例函数y=$\frac{k}{x}$的图象上，则k的值为$\sqrt{3}$．
20．下列各式，分解因式正确的是（ ）
| A． | a2-2ab+b2=（a-b）2 | B． | xy+xz+x=x（y+z） | C． | x2+x3=x3（$\frac{1}{x}$+1） | D． | a2+b2=（a+b）2 |
在正方形ABCO中，A（0，4），B（4，4），C（4，0），O（0，0），E为AO的中点，F为边CO上的动点，分别连接EF，FB，BE得到△EFB，并将其沿FB折叠得到△E′FB．