题目内容
10.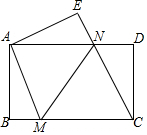 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落住点A处,点D落在点E处,直线MN交BC于点M,交AD于点N(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,DN=2,求MN的值.
分析 (1)连接AC,交MN于点O,根据轴对称的性质可得NA=NC,MA=MC,再根据∠ANM=∠AMN,可得AN=AM,进而得到NC=MC;
(2)过点N作NH⊥BC于点H,根据△CMN的面积与△CDN的面积比为3:1,DN=2,即可得出MC=3ND=6,CH=DN=2,再根据勾股定理,求得Rt△CHN中,NH=$\sqrt{C{N}^{2}-C{H}^{2}}$=4$\sqrt{2}$,即可得到Rt△MNH中,MN=$\sqrt{N{H}^{2}+M{H}^{2}}$=4$\sqrt{3}$.
解答  解:(1)如图,连接AC,交MN于点O,则MN⊥AC,且MN平分AC,
解:(1)如图,连接AC,交MN于点O,则MN⊥AC,且MN平分AC,
∴NA=NC,MA=MC,
由折叠可得∠AMN=∠CMN,
由AN∥CM可得∠ANM=∠CMN,
∴∠ANM=∠AMN,
∴AN=AM,
∴CM=CN;
(2)过点N作NH⊥BC于点H,则四边形NHCD是矩形. ∴HC=DN,NH=DC.
∴HC=DN,NH=DC.
∵△CMN的面积与△CDN的面积比为3:1,DN=2,
∴MC=3ND=6,CH=DN=2,
∴MH=4,而CN=CM=6,
∴Rt△CHN中,NH=$\sqrt{C{N}^{2}-C{H}^{2}}$=4$\sqrt{2}$,
∴Rt△MNH中,MN=$\sqrt{N{H}^{2}+M{H}^{2}}$=$\sqrt{32+16}$=4$\sqrt{3}$.
点评 此题考查了折叠的性质、矩形的性质、勾股定理以及平行线的性质的运用.解题时注意掌握辅助线的作法,构造直角三角形,运用勾股定理进行计算求解.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
20.下列调查中,适合用普查方式的是( )
| A. | 调查西安市市民的吸烟情况 | |
| B. | 调查西安市电视台某节目的收视率 | |
| C. | 调查西安市市民家庭日常生活支出情况 | |
| D. | 调查西安市某校某班学生对“文明西安”的知晓率 |
2.已知一次函数y=kx+5和y=k′x+1,假设k>0且k′<0,则这两个一次函数的图象的交点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列各式,分解因式正确的是( )
| A. | a2-2ab+b2=(a-b)2 | B. | xy+xz+x=x(y+z) | C. | x2+x3=x3($\frac{1}{x}$+1) | D. | a2+b2=(a+b)2 |
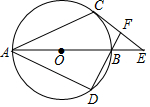 如图,AB为⊙O的直径,AC、AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为2,∠E=45°,则CF的长为4-2$\sqrt{2}$.
如图,AB为⊙O的直径,AC、AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为2,∠E=45°,则CF的长为4-2$\sqrt{2}$.