题目内容
在△ABC中,P是AB上的动点(P异于A、B),过点P的直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线 为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
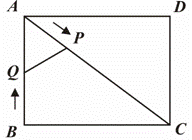
(1)如图①,∠A=90°,∠B=∠C,当BP=2PA时,P(l1)、P(l2)都是过点P的△ABC的相似线(其中l1⊥BC,l2∥AC),此外 ,还有 条;
,还有 条;
(2)如图②,∠C=90°,∠B=30°,当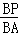
 = 时,P(lx)截得的三角形面积为△A
= 时,P(lx)截得的三角形面积为△A BC面积的
BC面积的
 .
.


(1)1; (2)
 或
或
 或
或

【解析】
试题分析:(1)存在另外 1 条相似线.
如图1所示,过点P 作l3∥BC交AC于Q,则△APQ∽△ABC;
作l3∥BC交AC于Q,则△APQ∽△ABC;
故答案为:1;

④第4条l4,此时AP与AC为对应边,且
 =
=
 ,∴
,∴
 =
=
 =
=
 ,∴
,∴
 =
=
 .
.
故答案为:
 或
或
 或
或
 .
.




考点:相似三角形的判定与性质.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作
中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作 DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。
DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。

 a(a为常数),求BK的长(用含a的代数式表示)。
a(a为常数),求BK的长(用含a的代数式表示)。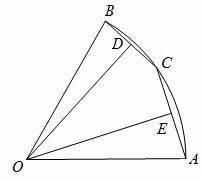


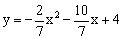 ,与x轴的另一交点为E,连结CE。
,与x轴的另一交点为E,连结CE。 的坐标;
的坐标;
 +1,AD=
+1,AD= 边形B′C′ED′,B′C′交AE于点F
边形B′C′ED′,B′C′交AE于点F ,则四边形B′FED′的面积为 ;
,则四边形B′FED′的面积为 ; ,将图
,将图 ②中的△AE
②中的△AE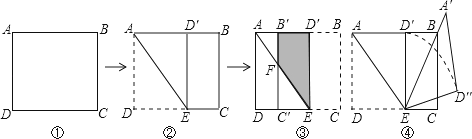
 )如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.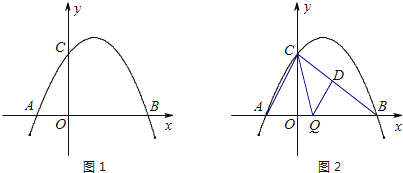
 点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).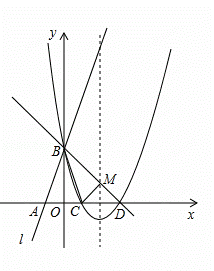

 点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标. 移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).