题目内容
如图,在半径为2的扇形AOB中,∠AOB=60°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域。
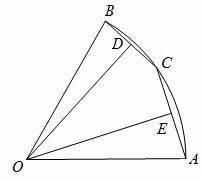
(1)∵点O是圆心,OD⊥BC,BC=1,∴BD= BC=
BC= 。
。
又∵OB=2,∴ 。
。


(3)∵BD=x,∴ 。
。
∵∠1=∠2,∠3=∠4,∠AOB=600。
∴∠DOE=∠2+∠3=30°。

如图2,过D作DF⊥OE,垂足为点F。
∴DF= OD=
OD= ,OF=
,OF= OD=
OD= 。
。
由△BOD∽△EDF,得 ,即
,即
 ,解得EF=
,解得EF= x。
x。
∴OE= 。
。
∴ 。
。
【考点】垂径定理,勾股定理,等边三角形的判定和性质,三角形中位线定理,相似三角形的判定和性质,含30度直角三角形的性质。


练习册系列答案
相关题目

 ,当
,当
 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.
 .试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
.试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
 CHGK是旋转过程中两块三角板的重叠部分(如图2).
CHGK是旋转过程中两块三角板的重叠部分(如图2).

 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由. 交y轴于点C,对称轴与x轴交于点D, 设点P(x,y)是该抛物线在x轴上方的一个动点(与点C不重合),△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围。
交y轴于点C,对称轴与x轴交于点D, 设点P(x,y)是该抛物线在x轴上方的一个动点(与点C不重合),△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围。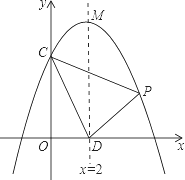

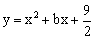 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点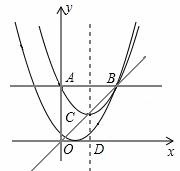
 时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)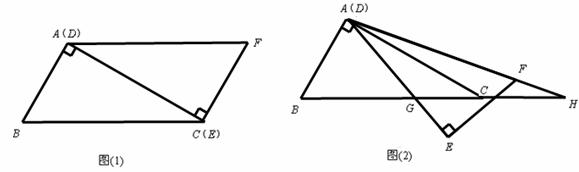
 为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
 ,还有 条;
,还有 条;
 = 时,P(lx)截得的三角形面积为△A
= 时,P(lx)截得的三角形面积为△A BC面积的
BC面积的
 .
.

 形时,t的值为 秒。
形时,t的值为 秒。