题目内容
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于 点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
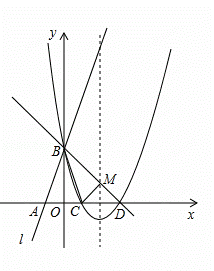

(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以 点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
(1)直线BD的解析式为:y=-x+3.抛物线的解析式为:y=x2-4x+3.(2)点N坐标为:(0,0),(-3,0)或(0,-3).点P的坐标为(4,3)或(-1,8).
【解析】

∴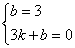
 ,
,
解得k=-1,b=3,
∴直线BD的解析式为:y=-x+3.
设抛物线的解析式为:y=a(x-1)(x-3),
∵点B(0,3)在抛物线上,
∴3=a×(-1)×( -3),
-3),
解得:a=1,
∴抛物线的解析式为:y=(x-1)(x-3)=x2-4x+3.

如答图1所示:


(Ⅰ)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);

(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(Ⅰ)当点P位于直线BD上方时,如答图2所示:




(Ⅱ)当点P位于直线BD下方时,如答图3所示:



过点P作PE⊥y轴于点E,则PE=m,OE=-n,BE=3-n.
S△PBD=S梯形PEOD+S△BOD-S△PB E=
E=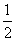
 (3+m)•(-n)+
(3+m)•(-n)+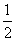
 ×3×3
×3×3 -
-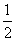
 (3-n)•m=6,
(3-n)•m=6,
化简得: m+n
m+n =-1 ②,
=-1 ②,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入②式整理得:m2-3m+4=0,△=-7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(-1,8).
考点:二次函数综合题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案 CHGK是旋转过程中两块三角板的重叠部分(如图2).
CHGK是旋转过程中两块三角板的重叠部分(如图2).

 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由. 为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
 ,还有 条;
,还有 条;
 = 时,P(lx)截得的三角形面积为△A
= 时,P(lx)截得的三角形面积为△A BC面积的
BC面积的
 .
.

 P逆时针
P逆时针 旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P
旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P CFE
CFE 的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
 边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.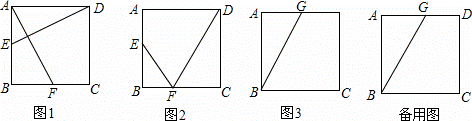


 ?若存在,求出t
?若存在,求出t 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.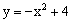 与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。 由。
由。
 形时,t的值为 秒。
形时,t的值为 秒。
 图1,已知直线y=kx与抛物线
图1,已知直线y=kx与抛物线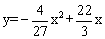
 交于点A(3,6).
交于点A(3,6).

 值?如果是,求出这个定值;如果不是,说明理由;
值?如果是,求出这个定值;如果不是,说明理由; 对称轴右侧的点
对称轴右侧的点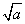
 -
-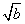
 0,∴a-2
0,∴a-2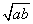
 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 立.
立.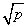
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2
 有最小值 ;
有最小值 ;

 x+1与x轴交于点A,过点A的另一直
x+1与x轴交于点A,过点A的另一直 线L2与双曲线y
线L2与双曲线y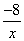

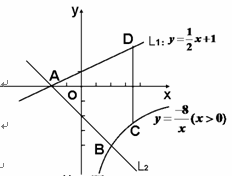

 D,试
D,试