题目内容
如图,以矩形ABCD的对角线AC的 中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作
中点O为圆心、OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K,过点D作 DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。
DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。


(1)求证:AE= CK
CK
(2)若AB=a,AD=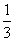
 a(a为常数),求BK的长(用含a的代数式表示)。
a(a为常数),求BK的长(用含a的代数式表示)。
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长。
(1)证明见解析;(2)
 ;(3)
;(3)
 ,6.
,6.
【解析】

试题解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD= BC,
BC,
∴∠DAE=∠BCK,
∵BK⊥AC,DH∥KB,
∴∠BKC=∠AED=90°,
∴△BKC≌△AD E,
E,
∴AE=CK;

(3)连结OG,


∵AC⊥DG,AC是⊙O的直径,DE=6,∴DE=EG=6,
又∵EF=FG,∴EF=3;

连接BG可得△BGF≌△AEF,AF=BF,△ADF≌△ BHF
BHF
∵AD=BC,BF∥CD,∴HF=DF,
∵FG=EF,∴HF-FG=DF-EF,∴HG=DE=6.
考点:1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.垂径定理.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目


 ,当
,当
 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.
 ,在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°,当点E是AB的中点时,线段DF的长度是 。
,在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°,当点E是AB的中点时,线段DF的长度是 。
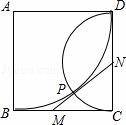
 方形,以A为圆心,AD为半径的圆弧与以CD为直径的半圆交于另一点P,过P作⊙A的切线分别交BC、CD于M、N两点,则
方形,以A为圆心,AD为半径的圆弧与以CD为直径的半圆交于另一点P,过P作⊙A的切线分别交BC、CD于M、N两点,则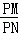
 = .
= .

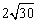 .试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
.试在直线a上找一点M,在直线c上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=【 】
 CHGK是旋转过程中两块三角板的重叠部分(如图2).
CHGK是旋转过程中两块三角板的重叠部分(如图2).

 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由. 为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
 ,还有 条;
,还有 条;
 = 时,P(lx)截得的三角形面积为△A
= 时,P(lx)截得的三角形面积为△A BC面积的
BC面积的
 .
.
