题目内容
1.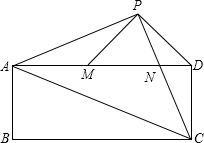 已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.(1)若AP=5,AB=$\frac{1}{3}$BC,求矩形ABCD的面积;
(2)若CD=PM,求证:AC=AP+PN.
分析 (1)根据勾股定理求出AC,设AB=x,BC=3x,在Rt△ABC中根据勾股定理求出AB、BC、即可求出答案;
(2)延长AP,CD交于Q,求出∠1=∠2,∠3=∠4,根据ASA证△APM≌△CPD,得出DP=PM=CD,求出∠Q=∠6,推出AC=AQ=AP+PQ,根据ASA证△APN≌△CPQ,推出PQ=PN,即可得出答案.
解答 (1)解:∵AP⊥CP且AP=CP,
∴△APC为等腰直角三角形,
∵AP=5,
∴AC=$\sqrt{2}$AP=5$\sqrt{2}$,
∵AB=$\frac{1}{3}$BC,
∴设AB=x,BC=3x,
∴在Rt△ABC中,
x2+(3x)2=(5$\sqrt{2}$)2,解得:x=$\sqrt{5}$,∴AB=$\sqrt{5}$,BC=3$\sqrt{5}$,
∴SABCD=AB•BC=$\sqrt{5}$×3$\sqrt{5}$=15;
(2)解:延长AP,CD交于Q,如图所示:
∵∠1+∠CND=∠2+∠PNA=90°,
且∠CND=∠ANP,
∴∠1=∠2,
又∠3+∠5=∠4+∠5=90°,
∴∠3=∠4,
在△APM和△CPD中,
$\left\{\begin{array}{l}{,1=∠2}&{\;}\\{AP=CP}&{\;}\\{∠3=∠4}&{\;}\end{array}\right.$,
∴△APM≌△CPD(ASA),
∴DP=PM,
又∵CD=PM,
∴CD=PD,
∴∠1=∠4=∠3,
∵∠1+∠Q=∠3+∠6=90°
∴∠Q=∠6
∴DQ=DP=CD
∴D为CQ中点,
又∵AD⊥CQ
∴AC=AQ=AP+PQ,
在△APN和△CPQ中,
$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{AP=CP}&{\;}\\{∠APC=∠CPQ}&{\;}\end{array}\right.$,
∴△APN≌△CPQ(ASA),
∴PQ=PN
∴AC=AP+PQ=AP+PN.
点评 本题考查了矩形的性质、全等三角形的性质和判定、三角形的内角和定理、等腰三角形的性质和判定、线段垂直平分线的性质等知识;题目综合性比较强,有一定的难度.

| A. | -7 | B. | 7 | C. | ±7 | D. | 49 |

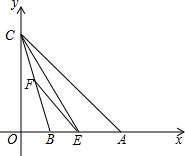 如图,在平面直角坐标系xOy中,已知点A的坐标为(6,0),点C的坐标为(0,6),tan∠CBO=$\frac{1}{3}$,E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.
如图,在平面直角坐标系xOy中,已知点A的坐标为(6,0),点C的坐标为(0,6),tan∠CBO=$\frac{1}{3}$,E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.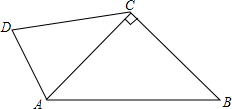 如图,在四边形ABCD中,AC⊥BC,且AC=BC,CD=4,若将线段DA绕点D按逆时针方形旋转90°得到DA′,连接BA′,则线段BA′的长度是4$\sqrt{2}$.
如图,在四边形ABCD中,AC⊥BC,且AC=BC,CD=4,若将线段DA绕点D按逆时针方形旋转90°得到DA′,连接BA′,则线段BA′的长度是4$\sqrt{2}$.